单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $M=\{x \mid 4-x < 0\}, N=\{x \mid 1 < x < 6, x \in Z\}$, 则 $M \cap N= $
$\text{A.}$ $\{2,3,4,5\}$
$\text{B.}$ $\{4,5,6\}$
$\text{C.}$ $\{4,5\}$
$\text{D.}$ $\{5\}$
已知复数 $z=2-2 i, \bar{z}$ 是 $z$ 的共轭复数, 则 $z \cdot \bar{z}= $
$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ $8$
$\text{C.}$ $4+4 i$
$\text{D.}$ $4-4 i$
已知 $a=6^{0.7}, b=0.7^{2022}, c=\log _{2021} \frac{1}{2022}$, 则
$\text{A.}$ $a>b>c$
$\text{B.}$ $a>c>b$
$\text{C.}$ $c>a>b$
$\text{D.}$ $b>a>c$
某学校对高三年级 500 名学生进行系统抽样, 编号分别为 $001,002, \ldots, 500$, 若样本相邻的 两个编号为 031,056 , 则样本中编号最大的为
$\text{A.}$ 479
$\text{B.}$ 480
$\text{C.}$ 481
$\text{D.}$ 482
$x^2>2021$ 是 $x^2>2022$ 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知实数 $x, y$ 满足
$$
\left\{\begin{array}{c}
x-y+1 \geq 0 \\
2 x-y-2 \leq 0 \\
x+y-1 \geq 0
\end{array}\right.
$$
则 $ z=2 x-3 y $ 的最小值为
$\text{A.}$ $3$
$\text{B.}$ $-3$
$\text{C.}$ $-6$
$\text{D.}$ $-7$
$\triangle A B C$ 为直角三角形, $\angle B=60^{\circ}, \angle A=90^{\circ}$, 则以 $A, B$ 为焦点且过点 $C$ 的椭圆的离心率为
$\text{A.}$ $\frac{\sqrt{3}}{2}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\sqrt{3}-1$
$\text{D.}$ $2-\sqrt{3}$
设等比数列 $\left\{a_n\right\}$ 满足 $a_1+a_3=20, a_2+a_4=10$, 则使 $a_1 \cdot a_2 \cdot a_3 \cdots a_n$ 最大的 $n$ 为
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 4 或 5
$\text{D.}$ 6
已知函数 $f(x)=a \cos 2 x+\sqrt{3} a \sin 2 x-2 a+b$ 在 $x \in\left[0, \frac{\pi}{2}\right]$ 上的图象如 右图所示, 则 $a, b$ 的值分别为
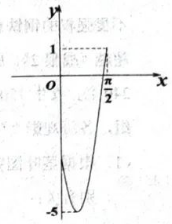
$\text{A.}$ $a=2, b=1$
$\text{B.}$ $a=2, b=3$
$\text{C.}$ $a=-2, b=-5$
$\text{D.}$ $a=-\frac{3}{2}, b=-2$
已知菱形 $A B C D$ 中, 满足 $A B=8, \overrightarrow{A B} \cdot \overrightarrow{A C}=32$, 若点 $G$ 在线段 $B D$ 上, 则 $\overrightarrow{G A} \cdot \overrightarrow{G B}$ 的最小值是
$\text{A.}$ -12
$\text{B.}$ 2
$\text{C.}$ 0
$\text{D.}$ -4
某几何体的三视图如右图所示, 则该几何体外接球的表面积为
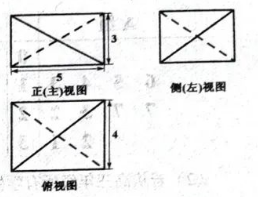
$\text{A.}$ $200 \pi$
$\text{B.}$ $100 \pi$
$\text{C.}$ $\frac{125}{2} \pi$
$\text{D.}$ $50 \pi$
已知不等式 $(k x+2 k) e^x < x+1$ 恰有 2 个整数解, 求实数 $k$ 的取值范围
$\text{A.}$ $\frac{3}{4 e^2} \leq k < \frac{2}{3 e}$
$\text{B.}$ $\frac{3}{4 e^2} < k \leq \frac{2}{3 e}$
$\text{C.}$ $\frac{4}{5 e^3} < k \leq \frac{3}{4 e^2}$
$\text{D.}$ $\frac{4}{5 e^3} \leq k < \frac{3}{4 e^2}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知 $a, b$ 均为正数且满足 $a+3 b=2$, 则 $\frac{1}{a}+\frac{5}{b}$ 的最小值为
已知数列 $\left\{a_n\right\}$ 是等差数列, $a_5=3$, 则 $S_9=$
已知平面向量 $\vec{a}, \vec{b}, \vec{c}$ 不共线且两两所成的角相等, $|\vec{a}|=|\vec{b}|=|\vec{c}|=2$, 则 $|\vec{a}+\vec{b}+\vec{c}|=$.
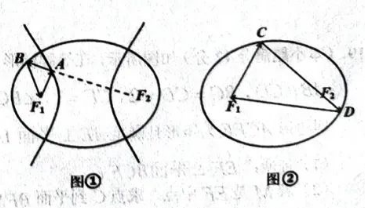
光线从椭圆的一个焦点发出, 被椭圆反射后会经过椭圆的另一个焦点; 光线从双曲线的一个 焦点发出, 被双曲线反射后的反射光线等效于从另一个焦点射出, 如图(1), 一个光学装置由 有公共焦点 $F_1 、 F_2$ 的椭圆 $\Gamma$ 与双曲线 $\Omega$ 构成, 现一光线从左焦点 $F_1$ 发出, 依次经 $\Omega$ 与 $\Gamma$ 反射, 又回到了点 $F_1$ ;历时 3 秒; 若将装 置中的 $\Omega$ 去掉, 如图(2), 此光线从点 $F_1$ 发出, 经 $\mathrm{F}$ 两次反射后又回到了点 $F_1$, 历时 $t$ 秒; 已知 $\Gamma$ 与 $\Omega$ 的离心率之比为 $2: 5$, 则 $t=$
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
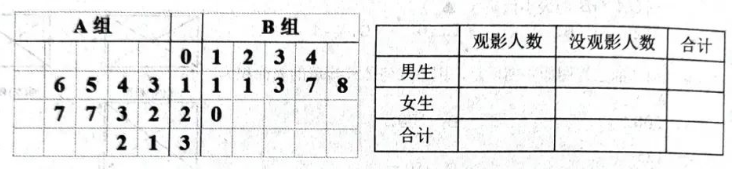
电影 《长津湖》让年轻人重新了解那一段历史, 见证中国人民爱国团结、 不畏强权的钢铁意志. 自上映以来, 已经打破了 29 项记录, 现总票房已经有 $56.98$ 亿, 已经 超越 《战狼 2 》, 成为中国电影历史排名的第 1 名. 某校高三年级 10 个班共 360 人, 其中男生 240 名, 女生 120 名, 现对学生观看 《长津湖》情况进行问卷调查, 各班观影男生人数记为 $A$ 组, 各班观影女生人数记为 $B$ 组, 得到如下茎叶图.
(1)根据茎叶图完成 $2 \times 2$ 列联表, 并判断是否有 $99 \%$ 的把握认为观看《长津湖》电影与性 别有关;
(2) 若从高三年级所有学生中按男女比例分层抽样选取 6 人参加座谈, 并从参加座谈的学生
中随机抽取 2 位同学赠送电影票, 求抽取的 2 位同学均为男生的概率.

已知 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$. 且 $b \sin B-a \sin A=(\sqrt{2} b-c) \sin (A+B)$.
(1) 求 $A$ 的大小;
(2) 过点 $C$ 作 $C D / / B A$, 在梯形 $A B C D$ 中, $B C=4, C D=3 \sqrt{3}, \angle A B C=120^{\circ}$, 求 $A D$ 的 长.
已知 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$. 且 $b \sin B-a \sin A=(\sqrt{2} b-c) \sin (A+B)$.
(1) 求 $A$ 的大小;
(2) 过点 $C$ 作 $C D / / B A$, 在梯形 $A B C D$ 中, $B C=4, C D=3 \sqrt{3}, \angle A B C=120^{\circ}$, 求 $A D$ 的 长.
如图所示, 在等腰梯形 $A B C D$ 中, $A B / / C D, B C=C D=2, C F=1, \angle B C D=120^{\circ}$, 四边形 $A C F E$ 为矩形且满足 $A E \perp$ 平面 $A B C D$.
(1) 证明: $E F \perp$ 平面 $B C F$ ;
(2) 若 $M$ 是 $E F$ 中点, 求点 $C$ 到平面 $B F M$ 的距离.

已知拋物线 $E: x^2=2 p y(p>0)$ 的焦点 $F$ 到准线的距离为 2 .
(1) 求拋物线 $E$ 的方程;
(2) 直线 $l: y=k x+1$ 与拋物线 $E$ 交于 $A, B$ 两点, 若以 $A B$ 为直径的圆与 $x=6$ 相切, 求实 数 $k$ 的值.
已知函数 $f(x)=\ln x+a x^2+1$.
(1) 若 $a=1$, 求 $f(x)$ 在 $P(1, f(1))$ 处的切线方程;
(2) 当 $0 < x \leq e^2$ 时, $g(x)=f(x)-a x^2-3+\frac{a}{x}$ 有最小值 2 , 求 $a$ 的值.
在直角坐标系 $x O y$ 中, 已知曲线 $C_1$ 的参数方程为
$\left\{\begin{array}{l}
x=\frac{a}{\cos \varphi}(\varphi \text { 为参数 }) \\
y=\tan \varphi
\end{array}\right.$ , $ a >0 $ 以坐标 原点为极点, $x$ 轴正半轴为极轴建立极坐标系, 曲线 $C_2$ 的极坐标方程为 $\rho=a \cos \theta$.
(1) 求曲线 $C_1$ 的普通方程和曲线 $C_2$ 的直角坐标方程;
(2) 已知点 $M$ 为曲线 $C_1$ 的右焦点, 点 $P$ 在曲线 $C_2$ 上, 且直线 $P M$ 与曲线 $C_2$ 相切, 若 $\sin \angle P M O=\frac{1}{2}$, 求实数 $a$ 的值.
已知函数 $f(x)=|2 x-a|-|2 x+3|, g(x)=|x-2|$.
(1)当 $a=1$ 时,解不等式 $f(x) \geq 2$ ;
(2)若 $f(x) \leq g(x)$ 在 $x \in[0,1]$ 时有解, 求实数 $a$ 的取值范围.