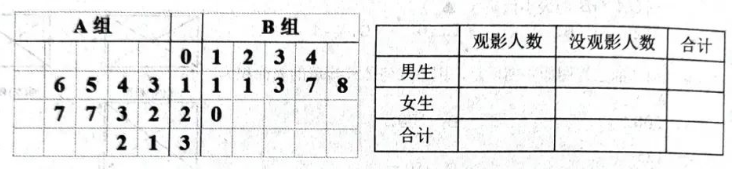
电影 《长津湖》让年轻人重新了解那一段历史, 见证中国人民爱国团结、 不畏强权的钢铁意志. 自上映以来, 已经打破了 29 项记录, 现总票房已经有 $56.98$ 亿, 已经 超越 《战狼 2 》, 成为中国电影历史排名的第 1 名. 某校高三年级 10 个班共 360 人, 其中男生 240 名, 女生 120 名, 现对学生观看 《长津湖》情况进行问卷调查, 各班观影男生人数记为 $A$ 组, 各班观影女生人数记为 $B$ 组, 得到如下茎叶图.
（1）根据茎叶图完成 $2 \times 2$ 列联表, 并判断是否有 $99 \%$ 的把握认为观看《长津湖》电影与性 别有关;


(2) 若从高三年级所有学生中按男女比例分层抽样选取 6 人参加座谈, 并从参加座谈的学生
中随机抽取 2 位同学赠送电影票, 求抽取的 2 位同学均为男生的概率.