单选题 (共 8 题 ),每题只有一个选项正确
集合 $A=\{x|| x-1 \mid < 1\}$, 集合 $B=\left\{y \mid y=x^2\right\}$, 则 $A \cap B=$
$\text{A.}$ $(0,2)$
$\text{B.}$ $[0,2)$
$\text{C.}$ $(-\infty, 2)$
$\text{D.}$ $(-1,2)$
已知 $z=(1-2 \mathrm{i})(3-\mathrm{i})$, 则 $z$ 对应的点在
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
已知 $\theta \in\left(\frac{3 \pi}{4}, \pi\right)$, 且 $\cos \theta-\sin \theta=-\frac{\sqrt{7}}{2}$, 则 $2 \sin \left(\frac{\pi}{4}+\theta\right)=$
$\text{A.}$ $-\frac{\sqrt{2}}{2}$
$\text{B.}$ $-\frac{1}{2}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{\sqrt{2}}{2}$
天干地支纪年法源于中国, 中国自古便有十天干与十二地支地支. 十天干即: 甲、乙、丙、 丁、戊、己、庚、辛、壬、癸; 十二地支即: 子、丑、寅、卯、辰、巳、午、末、申、 酉、戌、亥. 天干地支纪年法是按顺序以一个天干和一个地支相配, 排列起来, 天干在前, 地支在后, 天干由 “甲” 起, 地支由“子” 起, 比如第一年为 “甲子”, 第二年为 “乙丑”, 第三年为 “丙寅” $\cdots$, 以此类推, 排列到 “癸酉” 后, 天干回到 “甲” 重新开始, 即 “甲成”, “乙亥”, 之后地支回到 “子” 重新开始, 即 “丙子”, ..., 以此类推, 2023 年是癸卯年, 请问: 在 100 年后的 2123 年为
$\text{A.}$ 壬午年
$\text{B.}$ 癸末年
$\text{C.}$ 己亥年
$\text{D.}$ 戊戌年
在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, 已知 $A A_1=7$, 点 $O$ 在棱 $A A_1$ 上, 且 $A O=4, P$ 为 正方体表面上的动点, 若 $P O=5$, 则点 $P$ 的轨迹长度为
$\text{A.}$ $\frac{15 \pi}{2}$
$\text{B.}$ $(4+3 \sqrt{2} \pi)$
$\text{C.}$ $\frac{17 \pi}{2}$
$\text{D.}$ $(4+3 \sqrt{3}) \pi$
已知圆 $C:(x-5)^2+(y-12)^2=1$ 和两点 $A(0,-m), B(0, m)(m>0)$, 若圆 $C$ 上存在点 $P$, 使得 $\angle A P B=90^{\circ}$, 则 $m$ 的最小值为
$\text{A.}$ 14
$\text{B.}$ 13
$\text{C.}$ 12
$\text{D.}$ 11
已知 $x=4+2^{2.2}, y=6+\frac{8}{5} \ln 2, z=2^{3.1}$, 则
$\text{A.}$ $z>y>x$
$\text{B.}$ $y>x>z$
$\text{C.}$ $x>z>y$
$\text{D.}$ $z>x>y$
已知函数 $f(x)$ 的图像是连续不断的, 其定义域为 $(-1,1)$, 满足: 当 $x>0$ 时, $f(x)>0$; 任意的 $x, y \in(-1,1)$, 均有 $f(x+y)[1-f(x) f(y)]=f(x)+f(y)$. 若 $f(\ln x)>f\left(\frac{1}{2}\right)$, 则 $x$ 的取值范围是
$\text{A.}$ $\left(\frac{1}{\mathrm{e}}, \sqrt{\mathrm{e}}\right)$
$\text{B.}$ $\left(\frac{1}{\sqrt{\mathrm{e}}}, \sqrt{\mathrm{e}}\right)$
$\text{C.}$ $\left(\frac{1}{\mathrm{e}}, \frac{1}{\sqrt{\mathrm{e}}}\right) \cup(\sqrt{\mathrm{e}}, \mathrm{e})$
$\text{D.}$ $(\sqrt{\mathrm{e}}, \mathrm{e})$
多选题 (共 4 题 ),每题有多个选项正确
下列选项中判断正确的是
$\text{A.}$ 当 $x < \frac{5}{4}$ 时, $y=4 x-2+\frac{1}{4 x-5}$ 的最小值是 5
$\text{B.}$ 若关于 $x$ 的不等式 $a x^2+b x+c \leq 0$ 的解集是 $\{x \mid x \leq-2$ 或 $x \geq 6\}$, 则 $a+b+c>0$
$\text{C.}$ 已知向量 $\boldsymbol{a}=(2, m-1), \boldsymbol{b}=(m, 1)$, 若 $\boldsymbol{a} / / \boldsymbol{b}$, 则 $m=2$
$\text{D.}$ 已知向量 $\boldsymbol{a}=(1,3), b=(2, y),(a+b) \perp \boldsymbol{a}$, 则 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 的夹角为 $\frac{3 \pi}{4}$
已知函数 $f(x)=\frac{1}{2} \sin x+\sqrt{3} \cos ^2 \frac{x}{2}-\frac{\sqrt{3}}{2}$, 则
$\text{A.}$ $f(x)$ 的图象向右平移 $\frac{5 \pi}{6}$ 个单位长度后得到函数 $y=-\cos x$ 的图象
$\text{B.}$ $f(x)$ 的图象与 $g(x)=\sin \left(x+\frac{2 \pi}{3}\right)$ 的图象关于 $y$ 轴对称
$\text{C.}$ $f(x)$ 的单调递减区间为 $\left[2 k \pi+\frac{\pi}{6}, 2 k \pi+\frac{7 \pi}{6}\right](k \in \mathbf{Z})$
$\text{D.}$ $f(x)$ 在 $[0, a]$ 上有 3 个零点, 则实数 $a$ 的取值范围是 $\left[\frac{8 \pi}{3}, \frac{11 \pi}{3}\right]$.
如图, 正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 $1, P$ 是线段 $B C_1$ 上的动点, 则下列结论正确的是
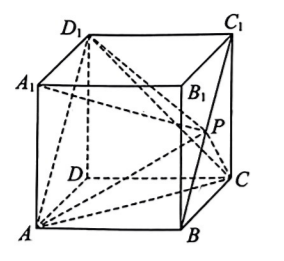
$\text{A.}$ 四面体 $A_1 D_1 A P$ 的体积为定值
$\text{B.}$ $A P+P C$ 的最小值为 $2 \sqrt{2}$
$\text{C.}$ $A_1 P / /$ 平面 $A C D_1$
$\text{D.}$ 当直线 $A_1 P$ 与 $A C$ 所成的角最大时, 四面体 $A_1 P C A$ 的外接球的体积为 $\frac{\sqrt{3}}{2} \pi$
平面直角坐标系 $x O y$ 中, 已知点 $P$ 在双曲线 $C: x^2-y^2=\lambda(\lambda>0)$ 的右支上运动, 平行四边形 $O A P B$ 的顶点 $A, B$ 分别在 $C$ 的两条渐近线上,则下列结论正确的为
$\text{A.}$ 直线 $A O, A P$ 的斜率之积为 -1
$\text{B.}$ 双曲线 $C$ 的离心率为 2
$\text{C.}$ $|P A|+|P B|$ 的最小值为 $\sqrt{2 \lambda}$
$\text{D.}$ 四边形 $O A P B$ 的面积可能为 $\frac{2 \lambda}{3}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
$(1-2 x)^{10}$ 的二项展开式中 $x$ 项的系数为
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $S_n=n+1$, 则数列 $\left\{a_n\right\}$ 的通项公式为
冬季两项是冬奥会的项目之一, 是把越野滑雪和射击两种不同特点的竞赛项目结合 在一起进行的运动. 其中冬季两项男子个人赛, 选手需要携带枪支和 20 发子弹, 每滑行 4 千米射击 1 次, 共射击 4 次, 每次 5 发子弹, 若每有 1 发子弹没命中, 则被罚 时 1 分钟, 总用时最少者获胜. 已知某男选手在一次比赛中共被罚时 3 分钟, 假设其射击时每发子弹命中的概率都相同, 且每发子弹是否命中相互独立, 记事件 $A$ 为 其在前两次射击中没有被罚时, 事件 $B$ 为其在第 4 次射击中被罚时 2 分钟, 那么 $P(A \mid B)=$
已知 $A 、 B 、 C$ 是椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 上的三个点, $O$ 为坐标原点, $A 、 B$ 两点 关于原点对称, $A C$ 经过右焦点 $F$, 若 $|O \vec{A}|=|\overrightarrow{O F}|$ 且 $\overrightarrow{A F}=2 \overrightarrow{F C}$, 则该椭圆的离心 率是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
数列 $\left\{a_n\right\}$ 是正项等比数列, 已知 $a_1=2$ 且 $a_3, 3 a_2, a_4$ 成等差数列.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 若 $b_n=\log _2 a_n, c_n=\frac{b_{n+1}^2-b_n}{b_n^2+b_n}$, 求数列 $\left\{c_n\right\}$ 的前 $n$ 项和 $S_n$.
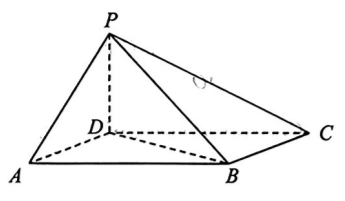
如图, 四棱锥 $P-A B C D$ 中, 底面 $A B C D$ 为 平行四边形, $\angle D A B=60^{\circ}, A B=2, A D=1$, $P D \perp$ 底面 $A B C D$.
(1) 证明: $P A \perp B D$;
(2) 若 $P D=A D$, 求二面角 $A-P B-C$ 的余 弦值.
请从① $a \sin B-\sqrt{3} b \cos B \cos C=\sqrt{3} c \cos ^2 B$; ② $(\sin A-\sin C)^2=\sin ^2 B-\sin A \sin C$;
③$\frac{\sqrt{3} b \sin A}{1+\cos B}=a$ 这三个条件中任选一个, 补充在下面问题中, 并加以解答(如末作出选 择, 则按照选择(1)评分. 选择的编号请填写到答题卡对应位置上).
在 $\triangle A B C$ 中, $a, b, c$ 分别是角 $A, B, C$ 的对边, 若
(1) 求角 $B$ 的大小:
(2) 若 $\triangle A B C$ 为锐角三角形, $c=1$, 求 $a^2+b^2$ 的取值范围.
2020 年, 是人类首次成功从北坡登顶珠峰 60 周年, 也是中国首次精确测定并公布珠峰高程的 45 周年. 华为帮助中国移动开通珠峰峰顶 $5 \mathrm{G}$, 有助于测量信号的实时开通, 为珠峰高程测量提供通信保障, 也验证了超高海拔地区 $5 \mathrm{G}$ 信号覆盖的可能性, 在持续高风速下 $5 \mathrm{G}$ 信号的稳定性, 在条件恶劣地区通过简易设备传输视频信号的可能性.正如任总在一次采访中所说: “华为公司价值体系的理想是为人类服务. ”有人曾问, “在珠峰 开通 5G 的意义在哪里? " 我认为它是科学技术的一次珠峰登顶, 告诉全世界, 华为 $5 \mathrm{G}$ 、 中国 $5 \mathrm{G}$ 的底气来自哪里! 现在 $5 \mathrm{G}$ 的到来给人们的生活带来更加颠覆性的变革, 某 IT 公 司基于领先技术的支持, $5 \mathrm{G}$ 经济收入在短期内逐月攀升, 该 IT 公司在 1 月份至 6 月份 的 $5 \mathrm{G}$ 经济收入 $y$ (单位: 百万元) 关于月份 $x$ 的数据如下表所示, 并根据数据绘制了如 下图所示的散点图.
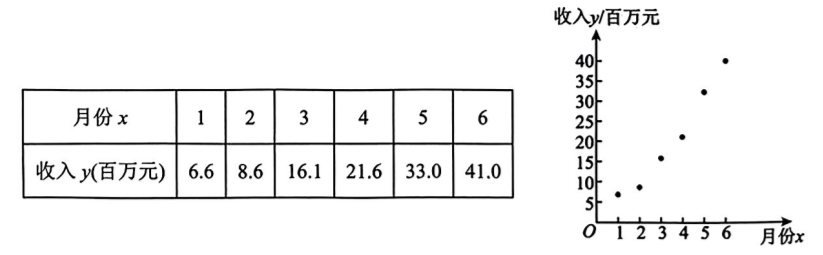
(1) 根据散点图判断, $y=a x+b$ 与 $y=c \cdot \mathrm{e}^{d x}(a, b, c, d$ 均为正常数)哪一个更适 宜作为 $5 G$ 经济收入 $y$ 关于月份 $x$ 的回归方程类型? (给出判断即可, 不必说明理由)
(2) 根据(1)的结果及表中的数据, 求出 $y$ 关于 $x$ 的回归方程, 并预测该公司 7 月份 的 5G 经济收入. (结果保留小数点后两位)
(3) 从前 6 个月的收入中抽取 2 个, 记收入超过 20 百万元的个数为 $X$, 求 $X$ 的分布 列和数学期望.
参考数据:
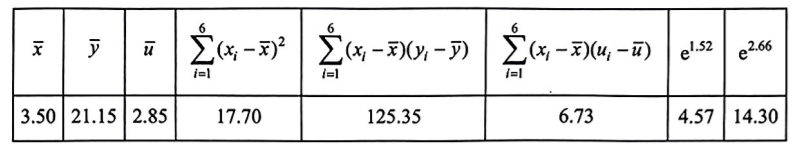
其中, 设 $u=\ln y, u_i=\ln y_i(i=1,2,3,4,5,6)$.
参考公式: 对于一组具有线性相关关系的数据 $\left(x_i, v_i\right)(i=1,2,3, \ldots, n)$,
其回归直线和最小而二乘估计分别为 $ \hat{\beta}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(v_i-\bar{v}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \text {, }$ $ \hat{\alpha}=\bar{v}-\hat{\beta} \bar{x} .$
抛物线 $C: y^2=2 p x(p>0)$ 上的点 $M\left(1, y_0\right)$ 到抛物线 $C$ 的焦点 $F$ 的距离为 $2, A 、 B$ (不与 $O$ 重合) 是抛物线 $C$ 上两个动点, 且 $O A \perp O B$.
(1) 求抛物线 $C$ 的标准方程;
(2) $x$ 轴上是否存在点 $P$ 使得 $\angle A P B=2 \angle A P O$ ? 若存在, 求出点 $P$ 的坐标, 若不存 在, 说明理由.
已知函数 $f(x)=\mathrm{e}^{a x}-x, g(x)=\sin x-\cos x-x+2$,
(1) 求函数 $f(x)$ 的单调区间;
(2) 若关于 $x$ 的不等式 $f(x) \geq g(x)$ 在 $x \in[0,+\infty)$ 上恒成立, 求实数 $a$ 的取值范围.