2020 年, 是人类首次成功从北坡登顶珠峰 60 周年, 也是中国首次精确测定并公布珠峰高程的 45 周年. 华为帮助中国移动开通珠峰峰顶 $5 \mathrm{G}$, 有助于测量信号的实时开通, 为珠峰高程测量提供通信保障, 也验证了超高海拔地区 $5 \mathrm{G}$ 信号覆盖的可能性, 在持续高风速下 $5 \mathrm{G}$ 信号的稳定性, 在条件恶劣地区通过简易设备传输视频信号的可能性.正如任总在一次采访中所说: “华为公司价值体系的理想是为人类服务. ”有人曾问, “在珠峰 开通 5G 的意义在哪里? " 我认为它是科学技术的一次珠峰登顶, 告诉全世界, 华为 $5 \mathrm{G}$ 、 中国 $5 \mathrm{G}$ 的底气来自哪里! 现在 $5 \mathrm{G}$ 的到来给人们的生活带来更加颠覆性的变革, 某 IT 公 司基于领先技术的支持, $5 \mathrm{G}$ 经济收入在短期内逐月攀升, 该 IT 公司在 1 月份至 6 月份 的 $5 \mathrm{G}$ 经济收入 $y$ (单位: 百万元) 关于月份 $x$ 的数据如下表所示, 并根据数据绘制了如 下图所示的散点图.



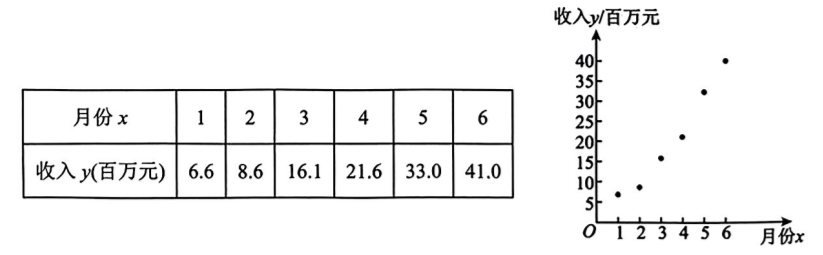
(1) 根据散点图判断, $y=a x+b$ 与 $y=c \cdot \mathrm{e}^{d x}(a, b, c, d$ 均为正常数）哪一个更适 宜作为 $5 G$ 经济收入 $y$ 关于月份 $x$ 的回归方程类型? （给出判断即可, 不必说明理由）
(2) 根据(1)的结果及表中的数据, 求出 $y$ 关于 $x$ 的回归方程, 并预测该公司 7 月份 的 5G 经济收入. (结果保留小数点后两位)
(3) 从前 6 个月的收入中抽取 2 个, 记收入超过 20 百万元的个数为 $X$, 求 $X$ 的分布 列和数学期望.
参考数据:


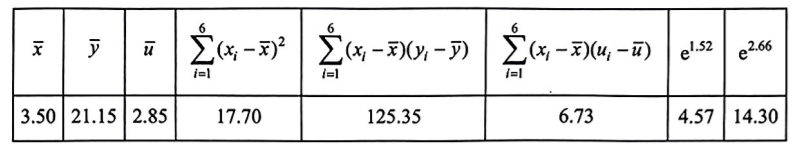
其中, 设 $u=\ln y, u_i=\ln y_i(i=1,2,3,4,5,6)$.
参考公式: 对于一组具有线性相关关系的数据 $\left(x_i, v_i\right)(i=1,2,3, \ldots, n)$,
其回归直线和最小而二乘估计分别为 $ \hat{\beta}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(v_i-\bar{v}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \text {, }$ $ \hat{\alpha}=\bar{v}-\hat{\beta} \bar{x} .$