解答题 (共 26 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
试问二元函数
$$
F(x, y)= \begin{cases}1 & x+y \geqslant 0 \\ 0 & x+y < 0\end{cases}
$$
能否成为某二维随机向量的联合分布函数?
设二维随机向量 $(X, Y)$ 的联合概率分布为
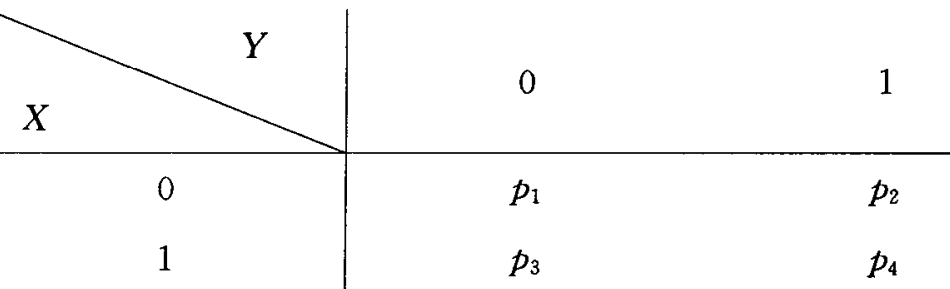
求 $(X, Y)$ 的联合分布函数.
设二维连续型随机向量 $(X, Y)$ 的密度函数为
$$
p(x, y)=\left\{\begin{array}{cc}
6 x y^2 & 0 < x < 1,0 < y < 1 \\
0 & \text { 其他 }
\end{array}\right.
$$
(1)求 $(X, Y)$ 的联合分布函数;
(2)求 $(X, Y)$ 的边际分布函数 $F_X(x)$ 和 $F_Y(y)$ ;
(3)判断 $X$ 和 $Y$ 是否独立。
设袋中装有 3 个白球, 2 个黑球及 1 个黄球,从中任取 4 个球,其中白球数记为 $X$ ,黑球数记为 $Y$ .求:
(1)$(X, Y)$ 的联合概率分布;
(2)$(X, Y)$ 的边际概率分布;
(3)$X$ 与 $Y$ 是否独立?
设二维随机向量 $(X, Y)$ 的联合密度函数为
$$
p(x, y)=\left\{\begin{array}{cc}
\frac{1}{8} x(x-y) & 0 \leqslant x \leqslant 2,|y| \leqslant x \\
0 & \text { 其他 }
\end{array}\right.
$$
求:(1)$P(X+Y \leqslant 2)$ ;
(2)关于 $X$ 与 $Y$ 的边际密度函数;
(3)讨论 $X$ 与 $Y$ 的独立性。
设随机变量 $X_1$ 和 $X_2$ 独立同分布,$P\left(X_1=k\right)=\frac{1}{3}, k=1,2,3$ ,且随机变量 $Y_1=\max \left\{X_1, X_2\right\}, Y_2=\min \left\{X_1, X_2\right\}$ 。
(1)求 $Y_1$ 与 $Y_2$ 的联合概率分布;
(2)判断 $Y_1$ 与 $Y_2$ 的独立性;
(3)求 $Y=Y_1 Y_2$ 的概率分布;
(4)求 $P\left(Y_1+Y_2 \leqslant 3\right), P\left(Y_1=Y_2\right)$ .
设 $(X, Y)$ 的联合密度函数为
$$
p(x, y)=\left\{\begin{array}{cc}
e^{-y} & 0 < x < 1, y>0 \\
0 & \text { 其他 }
\end{array}\right.
$$
(1)$X$ 与 $Y$ 是否独立?
(2)求 $X$ 与 $Y$ 的分布函数.
(3)求 $U=\max \{X, Y\}$ 和 $V=\min \{X, Y\}$ 的密度函数。
(4)求 $Z=2 X+Y$ 的密度函数.
设二维随机向量 $(X, Y)$ 在矩形 $G=\{(x, y) \mid 0 \leqslant x \leqslant 2$ , $0 \leqslant y \leqslant 1\}$ 上服从均匀分布,试求边长为 $X$ 和 $Y$ 的矩形面积 $S$ 的概率密度函数。
设 $(X, Y) \sim N(0,0,1,1,0)$ ,
(1)求 $P\left(X^2+Y^2 \leqslant a^2\right)$ ,其中 $a>0$ ;
(2)证明:
$$
\frac{1}{\sqrt{2 \pi}} \int_{-a}^a e^{-\frac{x^2}{2}} d x \leqslant \sqrt{1-e^{-a^2}}
$$
某疫苗每 1 毫升中所含细菌数服从参数为 1 的普阿松分布,把这种疫苗放人 5 只试管中,每只试管放 3 毫升疫苗,试求:
(1)每只试管中有细菌的概率;
(2)最多有 3 只试管中有细菌的概率。
下列二元函数 $F(x, y)$ 是否是某二维随机向量的联合分布函数?
$$
F(x, y)=\left\{\begin{array}{lc}
1 & x \geqslant 0, y \geqslant 0, x+y \geqslant 1 \\
0 & \text { 其他 }
\end{array}\right.
$$
一个袋中有 10 个球,其中有红球 4 个,白球 5 个和黑球 1 个,不放回地抽取两次,每次一球,记
$$
X_i= \begin{cases}0 & \text { 若第 } i \text { 次取到红球 } \\ 1 & \text { 若第 } i \text { 次取到白球 } i=1,2 \\ 2 & \text { 若第 } i \text { 次取到黑球 }\end{cases}
$$
求随机向量 $\left(X_1, X_2\right)$ 的联合概率分布,并且计算两次取到的球颜色相同的概率 $p$ .
随机地掷两颗骰子.设随机变量 $X$ 表示第一颗骰子出现的点数,随机变量 $Y$ 表示这两颗骰子出现点数的最大值,试求二维随机向量 $(X, Y)$ 的联合概率分布以及 $Y$ 的边际概率分布。
一个口袋中有三个球,依次标有数字 $1,2,2$ ,从中任取一个,不放回袋中,然后再任取一个.以 $X$ 和 $Y$ 分别表示第一次和第二次取到的球上标有的数字,求 $(X, Y)$ 的联合概率分布和联合分布函数.
设随机变量 $Y$ 服从参数为 $\lambda=1$ 的指数分布,定义随机变量 $X_1, X_2$ 为
$$
X_k=\left\{\begin{array}{ll}
0 & Y \leqslant k \\
1 & Y>k
\end{array} \quad k=1,2\right.
$$
求 $\left(X_1, X_2\right)$ 的联合概率分布.
设 $(X, Y)$ 在曲线 $y=x^2$ 和 $y=x$ 所围成的区域 $G$ 上服从二维均匀分布,求 $(X, Y)$ 的联合分布函数和边际密度函数,并讨论 $X$ 与 $Y$的独立性.
设 $X \sim U(0,1), Y \sim \operatorname{Exp}\left(\frac{1}{2}\right)$ ,且 $X$ 与 $Y$ 独立.求:
(1)$(X, Y)$ 的联合密度函数;
(2)设有关于 $t$ 的二次方程
$t^2+2 X t+Y=0$ ,求 $t$ 有实根的概率.
设 $(X, Y)$ 的联合密度函数为
$$
p(x, y)=\left\{\begin{array}{cc}
A x(1-x-y) & x>0, y>0, x+y < 1 \\
0 & \text { 其他 }
\end{array}\right.
$$
其中 $A$ 为待定常数,试求:
(1)常数 $A$ ;
(2)$X$ 和 $Y$ 是否独立?为什么?
(3)$P(Y>X)$ .
设二维连续型随机向量 $(X, Y)$ 的联合分布函数为
$$
F(x, y)=\left\{\begin{array}{cc}
1-e^{-x}-e^{-y}+e^{-(x+y)} & x>0, y>0 \\
0 & \text { 其他 }
\end{array}\right.
$$
求:(1)$(X, Y)$ 的联合密度函数;
(2)$(X, Y)$ 的边际密度函数,并讨论 $X$ 与 $Y$ 的独立性;
(3)$P((X, Y) \in D)$ ,其中 $D=\{(x, y) \mid 0 \leqslant x \leqslant 1,0 \leqslant y \leqslant x\}$ .
设 $(X, Y)$ 的联合密度函数为
$$
p(x, y)=\left\{\begin{array}{cc}
\frac{1}{2} \sin (x+y) & 0 < x < \frac{\pi}{2}, 0 < y < \frac{\pi}{2} \\
0 & \text { 其他 }
\end{array}\right.
$$
(1)求关于 $X$ 和 $Y$ 的边际密度函数;
(2)判断 $X$ 与 $Y$ 是否独立?
(3)求 $X$ 与 $Y$ 中至少有一个大于 $\frac{\pi}{4}$ 的概率 $p$ .
设 $(X, Y)$ 的联合密度函数为
$$
p(x, y)=\left\{\begin{array}{cc}
\frac{1+x y}{4} & |x| \leqslant 1,|y| \leqslant 1 \\
0 & \text { 其他 }
\end{array}\right.
$$
证明:(1)$X$ 与 $Y$ 不独立;
(2)$X^2$ 与 $Y^2$ 相互独立.
设随机向量 $(X, Y)$ 的联合密度函数为
$$
p(x, y)=\left\{\begin{array}{cc}
3 x & 0 < x < 1,0 < y < x \\
0 & \text { 其他 }
\end{array}\right.
$$
求 $Z=X-Y$ 的密度函数.
设随机向量 $(X, Y)$ 在矩形域 $D=\{(x, y) \mid 0 \leqslant x \leqslant 2,0 \leqslant y \leqslant 1\}$上服从二维均匀分布.记
$$
\begin{gathered}
U=\left\{\begin{array}{l}
0, X \leqslant Y \\
1, X>Y
\end{array}\right. \\
V=\left\{\begin{array}{l}
0, X \leqslant 2 Y \\
1, X>2 Y
\end{array}\right.
\end{gathered}
$$
求 $(U, V)$ 的联合概率分布.
设随机变量 $X$ 与 $Y$ 相互独立,$X$ 服从正态分布 $N\left(\mu, \sigma^2\right), Y$ 服从 $[-\pi, \pi]$ 上的均匀分布,试求 $Z=X+Y$ 的密度函数(计算结果用标准正态分布函数 $\Phi(x)$ 来表示)。
某商品一周的需求量是一个随机变量,其密度函数为
$$
p(x)=\left\{\begin{array}{cc}
x e^{-x} & x>0 \\
0 & x \leqslant 0
\end{array}\right.
$$
又设各周的需求量是相互独立的.试求:
(1)两周的需求量的密度函数;
(2)三周的需求量的密度函数.
测量某一零件长度的随机误差 $X$ 具有密度函数为 $p(x)=$ 152
$$
\frac{1}{2 \sqrt{2 \pi}} e^{-\frac{x^2}{8}}
$$
(1)求测量误差的绝对值不超过 1 的概率;
(2)独立地接连测量 3 次,求至少有 1 次误差的绝对值不超过 1 的概率;
(3)独立地接连测量 3 次,求平均误差的绝对值不超过 1 的概率.