一、单选题 (共 4 题 ),每题只有一个选项正确
1. 设积分 , 其中 , 若该积分收玫, 则必有
2. 设 , 其中符号函数
3. 设函数 连续, 则下列结论不成立的是
4. 设 , 则曲线积分
;
;
;
.
二、填空题 (共 17 题 ),请把答案直接填写在答题纸上
5. 计算积分 ,其中 为正整数.
6. 定积分
7. 定积分
8. 设 在 上可导, 且 , 其反函数为 , 满足
则 的表达式为
9. 定积分
10. (1) .
(2) .
(3) .
(4) .
11. (1) .
(2).
12. (1).
(2) .
(3) .
(4) .
13. (1).
(2) .
(3) .
14. (1) .
(2).
(3) .
15. (1) .
(2) .
(3) .
16. (1).
(2) .
(3) .
(4).
(5).
17. (1).
(2).
(3).
18. (1).
(2) .
三、解答题 (共 19 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
22. 设函数 在 上有连续的导数,且 , 证明 ,其中 .
23. 设 在 上具有连续导数,且 . 证明: 对于任意 , 有 .
24. 求极限 .
25. 在高中,我们学过了阶乘,其定义为
, 这里
为0或者正整数,其中规定
, 例如
, 那么你知道
是多少吗?
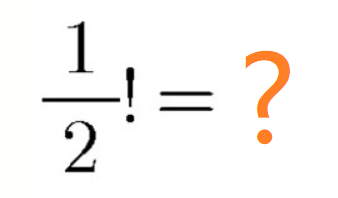
26. 计算下列不定积分
(1) .
(2) .
(3) .
27. 计算下列不定积分
(1) .
(2) .
28. 计算下列不定积分
(1) .
(2) .
(3) .
29. 计算下列不定积分
(1) .
(2) .
(3) .
(4) .
30. 计算下列不定积分
(1) .
(2) .
(3) .
(4) .
31. 设 为的一个原函数,求 .
34. 求
37.
40. 设 计算