单选题 (共 12 题 ),每题只有一个选项正确
计算 $(-6) \times\left(-\frac{1}{2}\right)$ 的结果是
$\text{A.}$ $-3$
$\text{B.}$ $3$
$\text{C.}$ $-12$
$\text{D.}$ $12$
下列运算正确的是
$\text{A.}$ $6 x-2 x=4$
$\text{B.}$ $a^{-2} \cdot a^{3}=a^{-6}$
$\text{C.}$ $x^{6} \div x^{3}=x^{3}$
$\text{D.}$ $(x-y)^{2}=x^{2}-y^{2}$
下列图形,其中轴对称图形的个数是

$\text{A.}$ 4
$\text{B.}$ 3
$\text{C.}$ 2
$\text{D.}$ 1
2022 年北京冬奥会国家速滑馆 “冰丝带” 屋顶上安装的光伏电站, 据测算, 每年可输出约 $44.8$ 万度的 清洁电力. 将 $44.8$ 万度用科学记数法可以表示为()
$\text{A.}$ $0.448 \times 10^{6}$ 度
$\text{B.}$ $44.8 \times 10^{4}$ 度
$\text{C.}$ $4.48 \times 10^{5}$ 度
$\text{D.}$ $4.48 \times 10^{6}$ 度
如图, $l_{1} / / l_{2}$, 点 $A$ 在直线 $l_{1}$ 上, 点 $B$ 在直线 $l_{2}$ 上, $A B=B C, \angle C=25^{\circ}, \angle 1=60^{\circ}$, 则 $\angle 2$ 的度 数是()
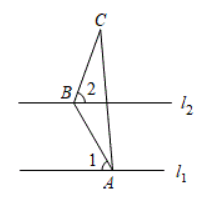
$\text{A.}$ $70^{\circ}$
$\text{B.}$ $65^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $55^{\circ}$
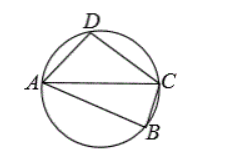
如图, $A B$ 是 $\odot O$ 的直径, $\angle A C D=\angle C A B, A D=2, A C=4$, 则 $\odot O$ 的半径为
$\text{A.}$ $2 \sqrt{3}$
$\text{B.}$ $3 \sqrt{2}$
$\text{C.}$ $2 \sqrt{5}$
$\text{D.}$ $\sqrt{5}$
某次射击比赛, 甲队员的成绩如图, 根据此统计图, 下列结论中错误的是
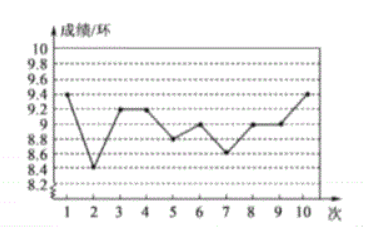
$\text{A.}$ 最高成绩是 $9.4$ 环
$\text{B.}$ 平均成绩是 9 环
$\text{C.}$ 这组成绩的众数是 9 环
$\text{D.}$ 这组成绩的方差是 $8.7$
如图, 四边形 $A B C D$ 中. $\angle A=60^{\circ}, A B / / C D, D E \perp A D$ 交 $A B$ 于点 $E$, 以点 $E$ 为圆心, $D E$ 为 半径, 且 $D E=6$ 的圆交 $C D$ 于点 $F$, 则阴影部分的面积为
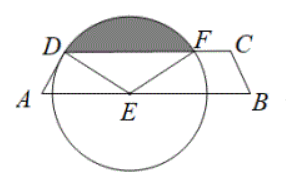
$\text{A.}$ $6 \pi-9 \sqrt{3}$
$\text{B.}$ $12 \pi-9 \sqrt{3}$
$\text{C.}$ $6 \pi-\frac{9 \sqrt{3}}{2}$
$\text{D.}$ $12 \pi-\frac{9 \sqrt{3}}{2}$
抛物线 $y=a x^{2}+b x+c$ 上部分点的横坐标 $x$, 纵坐标 $y$ 的对应值如表:
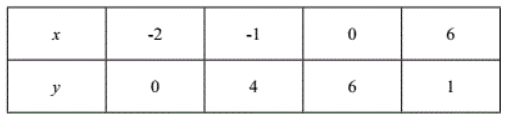
下列结论不正确的是()
$\text{A.}$ 抛物线的开口向下
$\text{B.}$ 抛物线的对称轴为直线 $x=\frac{1}{2}$
$\text{C.}$ 抛物线与 $x$ 轴的一个交点坐标为 $(2,0)$
$\text{D.}$ 函数 $y=a x^{2}+b x+c$ 的最大值为 $\frac{25}{4}$
我国古代著作 《四元玉鉴》记载 “买榢多少” 问题: “六贯二百一十钱, 遣人去买几株椽. 每株脚钱 三文足, 无钱准与一株椽. ”其大意为: 现请人代买一批椽, 这批椽的价钱为 6210 文. 如果每株榢的运 费是 3 文, 那么少拿一株楼后, 剩下的椽的运费恰好等于一株椽的价钱, 试问 6210 文能买多少株榢? 设 这批椽的数量为 $x$ 株, 则符合题意的方程是 ( )
$\text{A.}$ $3(x-1) x=6210$
$\text{B.}$ $3(x-1)=6210$
$\text{C.}$ $(3 x-1) x=6210$
$\text{D.}$ $3 x=6210$
如图, 平行四边形 $A B C D$ 的对角线 $A C, B D$ 相交于点 $O$. 点 $E$ 为 $B C$ 的中点, 连接 $E O$ 并延长交 $A D$ 于点 $F, \angle A B C=60^{\circ}, B C=2 A B$. 下列结论:(1) $A B \perp A C$ : (2) $A D=4 O E$ : (3)四边形 $A E C F$ 是菱形: (4) $S_{\triangle B O E}=\frac{1}{4} S_{\triangle A B C}$ 、其中正确结论的个数是
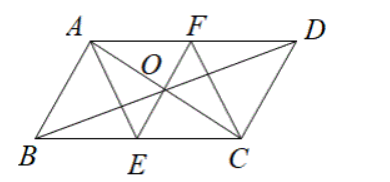
$\text{A.}$ 4
$\text{B.}$ 3
$\text{C.}$ 2
$\text{D.}$ 1
如图, 四边形 $A B C D$ 为矩形, $A B=3, B C=4$. 点 $P$ 是线段 $B C$ 上一动点, 点 $M$ 为线段 $A P$ 上一 点. $\angle A D M=\angle B A P$, 则 $B M$ 的最小值为 ( )

$\text{A.}$ $\frac{5}{2}$
$\text{B.}$ $\frac{12}{5}$
$\text{C.}$ $\sqrt{13}-\frac{3}{2}$
$\text{D.}$ $\sqrt{13}-2$
填空题 (共 13 题 ),请把答案直接填写在答题纸上
计算: $\sqrt{8} \cdot \sqrt{6}-3 \sqrt{\frac{4}{3}}=$.
如图, 四边形 $A B C D$ 为平行四边形, 则点 $B$ 的坐标为

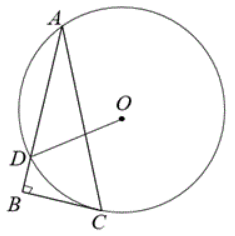
如图, 在 $\triangle A B C$ 中, $\angle B=90^{\circ}, \odot O$ 过点 $A 、 C$, 与 $A B$ 交于点 $D$, 与 $B C$ 相切于点 $C$, 若 $\angle A=32^{\circ}$, 则 $\angle A D O=$
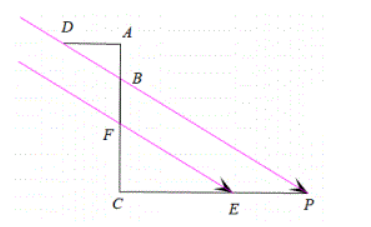
16. 如图, 某一时刻太阳光从窗户射入房间内, 与地面的夹角 $\angle D P C=30^{\circ}$, 已知窗户的高度 $A F=2 \mathrm{~m}$ , 穾台的高度 $C F=1 \mathrm{~m}$, 窗外水平遮阳篷的宽 $A D=0.8 \mathrm{~m}$, 则 $C P$ 的长度为 (结果精确到 0.1m ).
将从 1 开始的连续自然数按以下规律排列:
$\begin{array}{llcccccccc}\text { 第1行 } & & & & & 1 & & & & \\ \text { 第2行 } & & & & 2 & 3 & 4 & & & \\ \text { 第3行 } & & & 5 & 6 & 7 & 8 & 9 & & \\ \text { 第4行 } & & 10 & 11 & 12 & 13 & 14 & 15 & 16 & \\ \text { 第5行 } & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 & 25\end{array}$
若有序数对 $(n, m)$ 表示第 $n$ 行, 从左到右第 $m$ 个数, 如 $(3,2)$ 表示 6 , 则表示 99 的有序数对是
如图, 四边形 $A B C D$ 为正方形, 点 $E$ 是 $B C$ 的中点, 将正方形 $A B C D$ 沿 $A E$ 折叠, 得到点 $B$ 的对应 点为点 $F$, 延长 $E F$ 交线段 $D C$ 于点 $P$, 若 $A B=6$, 则 $D P$ 的长度为

1)化简: $\left(a-2-\frac{4}{a-2}\right) \div \frac{a-4}{a^{2}-4}$
(2) 化简: $2-\frac{5 x-2}{3}>\frac{3 x+1}{4}$
2022 年 3 月 23 日. “天宫课堂” 第二课开讲. “太空教师” 㺟志刚、王亚平、叶光富在中国空间站为 广大青少年又一次带来了精彩的太空科普课. 为了激发学生的航天兴趣, 某校举行了太空科普知识竞赛, 竞赛结束后随机抽取了部分学生成绩进行统计, 按成绩分为如下 5 组 (满分 100 分), $A$ 组: $75 \leq x < 80$, $B$ 组: $80 \leq x < 85 . C$ 组: $85 \leq x < 90, D$ 组: $90 \leq x < 95, E$ 组: $95 \leq x \leq 100$, 并绘制了如下不完 整的统计图. 请结合统计图, 解答下列问题:
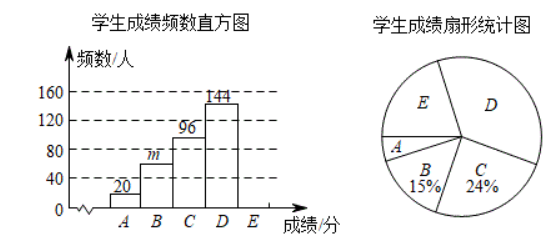
(1) 本次调查一共随机抽取了多少人?直方图m为多少?中位数落在哪组?
(2) 补全学生成绩频数直方图:
(3) 若成绩在 90 分及以上为优秀, 学校共有 3000 名学生, 估计该校成绩优秀的学生有多少人?
(4)学校将从获得满分的 5 名同学(其中有两名男生, 三名女生)中随机抽取两名, 参加周一国旗下的 演讲, 请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.
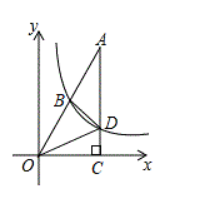
如图, 点 $A$ 在第一象限, $A C \perp x$ 轴, 垂足为 $C, O A=2 \sqrt{5}, \tan A=\frac{1}{2}$, 反比例函数 $y=\frac{k}{x}$ 的图像
经过 $O A$ 的中点 $B$, 与 $A C$ 交于点 $D$.
(1) 求 $k$ 值;
(2) 求 $\triangle O B D$ 的面积.
泰安某茶叶店经销泰山女儿茶, 第一次购进了 $A$ 种茶 30 盒, $B$ 种茶 20 盒, 共花费 6000 元: 第二次购进时, 两种杀每盒的价格都提高了 $20 \%$, 该店又购进了 $A$ 种杀 20 盒, $B$ 种杀 15 盒, 共花费 5100 元. 求 第一次购进的 $A 、 B$ 两种茶每盒的价格.
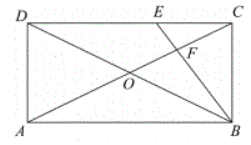
如图, 矩形 $A B C D$ 中, 点 $E$ 在 $D C$ 上, $D E=B E, A C$ 与 $B D$ 相交于点 $O$. $B E$ 与 $A C$ 相交于点 $F$.
(1) 若 $B E$ 平分 $\angle C B D$, 求证: $B F \perp A C$;
(2)找出图中与 $\triangle O B F$ 相似的三角形, 并说明理由;
(3) 若 $O F=3, E F=2$, 求 $D E$ 的长度.
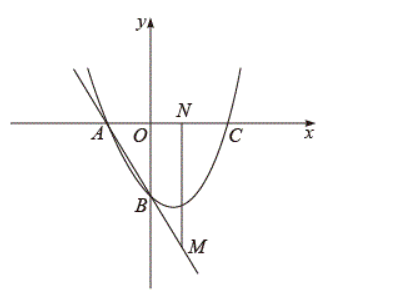
若二次函数 $y=a x^{2}+b x+c$ 的图象经过点 $A(-2,0), B(0,-4)$, 其对称轴为直线 $x=1$, 与 $x$ 轴的另 一交点为C
(1) 求二次函数的表达式:
(2) 若点 $M$ 在直线 $A B$ 上, 且在第四象限, 过点 $M$ 作 $M N \perp x$ 轴于点 $N$.
(1)若点 $N$ 在线段 $O C$ 上, 且 $M N=3 N C$, 求点 $M$ 的坐标;
(2)以 $M N$ 为对角线作正方形 $M P N Q$ (点 $P$ 在 $M N$ 右侧), 当点 $P$ 在抛物线上时, 求点 $M$ 的坐标.
(1) 在 $\triangle A B C$ 中, $B D, C E$ 分别是 $\angle A B C$ 与 $\angle B C A$ 的平分线.
① 若 $\angle A=60^{\circ}, A B=A C$, 如图, 试证明 $B C=C D+B E$ :
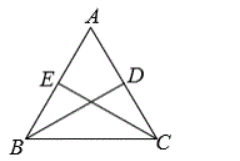
② 将① 中的条件 “ $A B=A C ”$ 去掉, 其他条件不变, 如图, 问① 中的结论是否成立? 并说明理由.
(2) 若四边形 $A B C D$ 是圆的内接四边形, 且 $\angle A C B=2 \angle A C D, \angle C A D=2 \angle C A B$, 如图, 试探究线 段 $A D, B C, A C$ 之间的等量关系, 并证明.