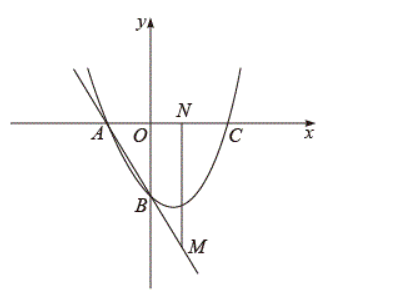
若二次函数 $y=a x^{2}+b x+c$ 的图象经过点 $A(-2,0), B(0,-4)$, 其对称轴为直线 $x=1$, 与 $x$ 轴的另 一交点为C
(1) 求二次函数的表达式:
(2) 若点 $M$ 在直线 $A B$ 上, 且在第四象限, 过点 $M$ 作 $M N \perp x$ 轴于点 $N$.
(1)若点 $N$ 在线段 $O C$ 上, 且 $M N=3 N C$, 求点 $M$ 的坐标;
(2)以 $M N$ 为对角线作正方形 $M P N Q$ (点 $P$ 在 $M N$ 右侧), 当点 $P$ 在抛物线上时, 求点 $M$ 的坐标.