(1) 在 $\triangle A B C$ 中, $B D, C E$ 分别是 $\angle A B C$ 与 $\angle B C A$ 的平分线.
① 若 $\angle A=60^{\circ}, A B=A C$, 如图, 试证明 $B C=C D+B E$ :
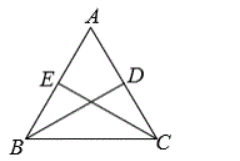
② 将① 中的条件 “ $A B=A C ”$ 去掉, 其他条件不变, 如图, 问① 中的结论是否成立? 并说明理由.
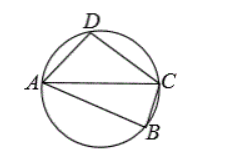
(2) 若四边形 $A B C D$ 是圆的内接四边形, 且 $\angle A C B=2 \angle A C D, \angle C A D=2 \angle C A B$, 如图, 试探究线 段 $A D, B C, A C$ 之间的等量关系, 并证明.
① 若 $\angle A=60^{\circ}, A B=A C$, 如图, 试证明 $B C=C D+B E$ :

② 将① 中的条件 “ $A B=A C ”$ 去掉, 其他条件不变, 如图, 问① 中的结论是否成立? 并说明理由.
(2) 若四边形 $A B C D$ 是圆的内接四边形, 且 $\angle A C B=2 \angle A C D, \angle C A D=2 \angle C A B$, 如图, 试探究线 段 $A D, B C, A C$ 之间的等量关系, 并证明.
