单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $A=\left\{x \in N^* \mid y=\sqrt{4-x^2}\right\}$, 集合 $B=\left\{x \mid x^2-x \geq 0\right\}$, 则 $A \cap B=$
$\text{A.}$ $\{x \mid 1 \leq x \leq 2\}$
$\text{B.}$ $\{x \mid 0 \leq x \leq 1\}$
$\text{C.}$ $\{0,1,2\}$
$\text{D.}$ $\{1,2\}$
复数 $z$ 满足 $i^5 \cdot z=1+i$, 则 $z$ 在复平面内对应的点位于
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
已知向量 $\vec{a}=(-1,2), \vec{b}=(3,-1), \vec{c}=(x, 1)$, 且 $(\vec{a}+2 \vec{b}) \perp \vec{c}$, 则 $x=$
$\text{A.}$ 2
$\text{B.}$ 1
$\text{C.}$ 0
$\text{D.}$ -1
“函数 $f(x)=x^a$ 在 $(0,+\infty)$ 上单调递减” 是 “函数 $g(x)=x^4-(a+1) x$ 是偶函数” 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
在平面直角坐标系中, 过直线 $2 x-y-3=0$ 上一点 $P$ 作圆 $O: x^2+2 x+y^2=1$ 的两条切 线, 切点分别为 $A 、 B$, 则 $\sin \angle A P B$ 的最大值为
$\text{A.}$ $\frac{2 \sqrt{6}}{5}$
$\text{B.}$ $\frac{2 \sqrt{5}}{5}$
$\text{C.}$ $\frac{\sqrt{6}}{5}$
$\text{D.}$ $\frac{\sqrt{5}}{5}$
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别是 $F_1, F_2$, 点 $P$ 是椭圆 $C$ 上位于第 一象限的一点, 且 $P F_2$ 与 $y$ 轴平行, 直线 $P F_1$ 与 $C$ 的另一个交点为 $Q$, 若 $2 \overrightarrow{P F_1}=5 \overrightarrow{F_1 Q}$, 则 $C$ 的离心率为
$\text{A.}$ $\frac{\sqrt{21}}{7}$
$\text{B.}$ $\frac{\sqrt{33}}{11}$
$\text{C.}$ $\frac{\sqrt{7}}{7}$
$\text{D.}$ $\frac{\sqrt{21}}{11}$
若数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n, 2 S_n a_n=a_n{ }^2+1\left(n \in N^*, a_n>0\right)$, 则下列结论正确的是
$\text{A.}$ $a_{2022} a_{2023}>1$
$\text{B.}$ $a_{2023}>\sqrt{2023}$
$\text{C.}$ $S_{2023} < \sqrt{2022}$
$\text{D.}$ $\frac{1}{S_1}+\frac{1}{S_2}+\frac{1}{S_3}+\cdots+\frac{1}{S_{100}} < 19$
已知函数 $f(x)=3 \cos (\omega x+\varphi)(\omega>0)$, 若 $f\left(-\frac{\pi}{4}\right)=3, f\left(\frac{\pi}{2}\right)=0$, 在区间 $\left(-\frac{\pi}{3},-\frac{\pi}{6}\right)$ 上 没有零点, 则 $\omega$ 的取值共有
$\text{A.}$ 4个
$\text{B.}$ 5个
$\text{C.}$ 6个
$\text{D.}$ 7个
多选题 (共 4 题 ),每题有多个选项正确
下列关于概率统计说法中正确的是
$\text{A.}$ 两个变量 $x, y$ 的相关系数为 $r$, 则 $r$ 越小, $x$ 与 $y$ 之间的相关性越弱
$\text{B.}$ 设随机变量 $\xi: N(2,1)$, 若 $p(\xi>3)=p$, 则 $p(1 < \xi < 2)=\frac{1}{2}-p$
$\text{C.}$ 在回归分析中, $R^2$ 为 0.89 的模型比 $R^2$ 为 0.98 的模型拟合得更好
$\text{D.}$ 某人解答 10 个问题, 答对题数为 $X, X \sim B(10,0.8)$, 则 $E(X)=8$
对数的发明是数学史上的重大事件. 我们知道, 任何一个正实数 $N$ 可以表示成 $N=a \times 10^n(1 \leq a < 10, n \in \mathbf{Z})$ 的形式, 两边取常用对数, 则有 $\lg N=n+\lg a$, 现给出部分常 用对数值 (如下表), 下列结论正确的是
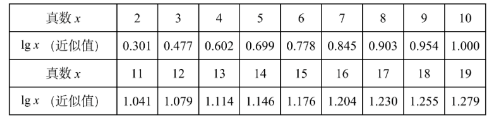
$\text{A.}$ $5^{10}$ 在区间 $\left(10^6, 10^7\right)$ 内
$\text{B.}$ $3^{50}$ 是 15 位数
$\text{C.}$ 若 $7^{-50}=a \times 10^m$, 则 $m=-43$
$\text{D.}$ 若 $m^{30}\left(m \in N^*\right)$ 是一个 35 位正整数, 则 $m=14$
菱形 $A B C D$ 的边长为 $a$, 且 $\angle B A D=60^{\circ}$, 将 $\triangle A B D$ 沿 $B D$ 向上翻折得到 $\triangle P B D$, 使二 面角 $P-B D-C$ 的余弦值为 $\frac{1}{3}$, 连接 $P C$, 球 $O$ 与三棱雉 $P-B C D$ 的 6 条棱都相切, 下列结论正确的是
$\text{A.}$ $P O \perp$ 平面 $B C D$
$\text{B.}$ 球 $O$ 的表面积为 $2 \pi a^2$
$\text{C.}$ 球 $O$ 被三棱雉 $P-B C D$ 表面截得的截面周长为 $\frac{4 \sqrt{3}}{3} \pi a$
$\text{D.}$ 过点 $O$ 与直线 $P B, C D$ 所成角均为 $\frac{\pi}{4}$ 的直线可作 4 条
已知函数 $f(x)$ 与 $g(x)$ 的定义域均为 $R, f(x+1)+g(x-2)=3, f(x-1)-g(-x)=1$, 且 $g(-1)=2, g(x-1)$ 为偶函数, 下列结论正确的是
$\text{A.}$ 4 为 $f(x)$ 的一个周期
$\text{B.}$ $g(3)=1$
$\text{C.}$ $\sum_{k=1}^{2023} f(k)=4045$
$\text{D.}$ $\sum_{k=1}^{2023} g(k)=2023$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
为全面推进乡村振兴, 永州市举办了 “村晚兴乡村” 活动, 晚会有 《走, 去永州》《扬 鞭催卫运粮忙》《数幸福》《乡村振兴唱起来》四个节目, 若要对这四个节目进行排 序, 要求《数幸福》与《乡村振兴唱起来》相邻, 则不同的排列种数为 (用 数字作答).
在平行六面体 $A B C D-A_1 B_1 C_1 D_1$ 中, $\overrightarrow{D A}=\vec{a}, \overrightarrow{D C}=\vec{b}, \overrightarrow{D D_1}=\vec{c}, P$ 为 $D D_1$ 的中点, 过 $P B$ 的平面 $a$ 分别与棱 $A A_1, C C_1$ 交于点 $E, F$, 且 $A E=C F$, 则 $\overrightarrow{B P}+\overrightarrow{E F}=$ (用 $\vec{a}, \vec{b}, \vec{c}$ 表示).
若函数 $f(x)=\frac{\left(e^{t x}+2\right) t x}{x+2}-\ln x$, 当 $x \in(0,+\infty)$ 时, $f(x)>0$, 则实数 $t$ 的取值范围
已知点 $N(a, 2 \sqrt{3})(a>0)$ 在抛物线 $C: y^2=2 p x(0 < p < 2 a)$ 上, $F$ 为抛物线 $C$ 的焦点, 圆 $N$ 与直线 $x=\frac{p}{2}$ 相交于 $A 、 B$ 两点, 与线段 $N F$ 相交于点 $R$, 且 $|A B|=2 \sqrt{5}|R F|$. 若 $R$ 是线段 $N F$ 上靠近 $F$ 的四等分点, 则抛物线 $C$ 的方程为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left\{a_n\right\}$ 是公比 $q>1$ 的等比数列, 前三项和为 39 , 且 $a_1, a_2+6, a_3$ 成等差数列.
(1)求数列 $\left\{a_n\right\}$ 的通项公式;
(2)设 $b_n=\frac{1}{\log _3 a_{2 n-1} \cdot \log _3 a_{2 n+1}}\left(n \in N^{\star}\right)$, 求 $\left\{b_n\right\}$ 的前 $n$ 项和 $T_n$.
在 $\triangle A B C$ 中, 设 $A, B, C$ 所对的边分别为 $a, b, c$, 且满足 $c \cos A-a \cos C=a+b$.
(1) 求角 $C$;
(2)若 $c=5, \triangle A B C$ 的内切圆半径 $r=\frac{\sqrt{3}}{4}$, 求 $\triangle A B C$ 的面积.
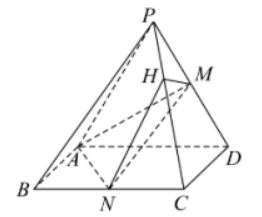
19. 如图所示, 在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 为矩形, 侧面 $P A D$ 为正三角形, 且 $A D=2 A B=4, M 、 N$ 分别为 $P D 、 B C$ 的中点, $H$ 在线段 $P C$ 上, 且 $P C=3 P H$.
(1)求证: $M N / /$ 平面 $P A B$;
(2)当 $A M \perp P C$ 时, 求平面 $A M N$ 与平面 $H M N$ 的夾角的余弦值.
某企业为提高竞争力, 成功研发了三种新品 $A, B, C$, 其中 $A 、 B 、 C$ 能通过行业标准 检测的概率分别为 $\frac{4}{5}, \frac{6}{7}, \frac{9}{10}$, 且 $A, B, C$ 是否通过行业标准检测相互独立.
(1)设新品 $A 、 B 、 C$ 通过行业标准检测的品种数为 $X$, 求 $X$ 的分布列;
(2)已知新品 $A$ 中的一件产品经检测认定为优质产品的概率为 0.025 , 现从足量的新品 $A$ 中任意抽取一件进行检测, 若取到的不是优质产品, 则继续抽取下一件, 直至取到 优质产品为止, 但抽取的总次数不超过 $n$. 如果抽取次数的期望值不超过 5 , 求 $n$ 的 最大值.
参考数据: $0.975^4 \approx 0.904,0.975^5 \approx 0.881,0.975^6 \approx 0.859,0.975^7 \approx 0.838,0.975^8 \approx 0.817$
已知点 $A$ 为圆 $C: x^2+y^2-2 \sqrt{10} x-6=0$ 上任意一点, 点 $B$ 的坐标为 $(-\sqrt{10}, 0)$, 线段 $A B$ 的垂直平分线与直线 $A C$ 交于点 $D$.
(1)求点 $D$ 的轨迹 $E$ 的方程;
(2)设轨迹 $c$ 与 $x$ 轴分别交于 $A_1 、 A_2$ 两点 ( $A_1$ 在 $A_2$ 的左侧), 过 $R(3,0)$ 的直线 $l$ 与轨 迹 $E$ 交于 $M 、 N$ 两点, 直线 $A_1 M$ 与直线 $A_2 N$ 的交于 $P$, 证明: $P$ 在定直线上.
已知函数 $f(x)=\ln (x+1), g(x)=a x e^x-2 \ln a+3 \ln 2+3$.
(1)当 $x \in(-1,0) \cup(0,+\infty)$ 时, 求证: $\frac{f(x)}{x}>-\frac{1}{2} x+1$;
(2) 若 $x \in(-1,+\infty)$ 时, $g(x) \geq f(x)$, 求实数 $a$ 的取值范围.