科数网

对数的发明是数学史上的重大事件. 我们知道, 任何一个正实数

N

可以表示成

N = a \times 10^{n} (1 \leq a < 10, n \in Z)

的形式, 两边取常用对数, 则有

\lg N = n + \lg a

, 现给出部分常用对数值 (如下表), 下列结论正确的是

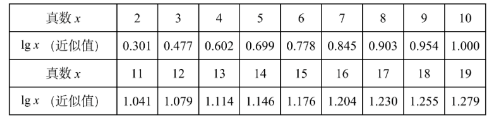
A.

5^{10}

在区间

(10^{6}, 10^{7})

内

B.

3^{50}

是 15 位数

C.

若

7^{- 50} = a \times 10^{m}

, 则

m = - 43

D.

若

m^{30} (m \in N^{*})

是一个 35 位正整数, 则

m = 14

0 人点赞 153 次查看白板加入试卷

答案与解析：

答案仅限会员可见微信内自动登录或手机登录或微信扫码注册登录点击我要开通VIP