单选题 (共 8 题 ),每题只有一个选项正确
若集合 $A=\left\{x \mid 3 x^2-5 x-8 < 0\right\}, B=\left\{y \mid y=x^2-4 x+5\right\}$, 则 $A \cap B=$
$\text{A.}$ $[-1,1)$
$\text{B.}$ $\left[1, \frac{8}{3}\right)$
$\text{C.}$ $\left(-1, \frac{8}{3}\right)$
$\text{D.}$ $\left(1, \frac{8}{3}\right)$
为了迎接学校即将到来的某项活动, 某班组织学生进行卫生大扫除, 班主任将班级中的 9 名同学平均分配 到三个包干区 (编号 1、2、3) 进行卫生打扫, 其中甲同学必须打扫 1 号包于区, 则不同的分配方法有
$\text{A.}$ 560 种
$\text{B.}$ 280 种
$\text{C.}$ 840 种
$\text{D.}$ 1120 种
设 $m \in \mathbf{R}$, 则 “ $m=2$ ” 是 “ $\frac{3+m^2 \mathrm{i}}{2-\mathrm{i}}+m\left(\frac{1}{5}+\frac{\mathrm{i}}{5}\right)(3+4 \mathrm{i})$ 为纯虚数”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知函数 $f(x)=x^\alpha, g(x)=x^\beta$, 其中 $x \in[0,+\infty), 0 < a < 1, \beta>1$, 若点 $M\left(\frac{1}{2}, f\left(\frac{1}{2}\right)\right), N\left(\frac{1}{4}, f\left(\frac{1}{4}\right)\right)$, $P\left(\frac{1}{2}, g\left(\frac{1}{2}\right)\right), Q\left(\frac{1}{4}, g\left(\frac{1}{4}\right)\right)$ 满足 $|M P|=|N Q|$, 则
$\text{A.}$ $4^\alpha-4^{\beta}=2^{a+\beta}$
$\text{B.}$ $4^a+4^{\beta}=2^{a-\beta}$
$\text{C.}$ $2^{\alpha}-2^\beta=2^{\alpha+\beta}$
$\text{D.}$ $2^\alpha+2^{\beta}=2^{\alpha+\beta}$
已知首项为 3 的数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 若 $a_n S_{n+1}+2=a_n\left(S_n+2\right)$, 则 $S_{2023}=$
$\text{A.}$ 1435
$\text{B.}$ 1436
$\text{C.}$ $\frac{8603}{6}$
$\text{D.}$ $\frac{4307}{3}$
已知菱形 $A B C D$ 的边长为 4 , 点 $E, F$ 分别是线段 $C D, A D$ 上靠近点 $D, A$ 的三等分点, 若 $\overrightarrow{A B} \cdot \overrightarrow{A C}=8$, 则 $\overrightarrow{A E} \cdot \overrightarrow{B F}=$
$\text{A.}$ $\frac{64}{9}$
$\text{B.}$ $-\frac{64}{9}$
$\text{C.}$ $\frac{16}{3}$
$\text{D.}$ $-\frac{16}{3}$
已知函数 $f(x)=\frac{1}{2^x+2}+\frac{2}{4^z-4}+1+\frac{1}{x-1}$, 则不等式 $f(2 x+3)>f\left(x^2\right)$ 的解集为
$\text{A.}$ $(-2,1) \cup(1,+\infty)$
$\text{B.}$ $(-1,1) \cup(3,+\infty)$
$\text{C.}$ $\left(-\frac{1}{2}, 1\right) \cup(3,+\infty)$
$\text{D.}$ $(-3,1) \cup(3,+\infty)$
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1, F_2$, 点 $M, N$ 在双曲线 $C$ 上, $P(-a, 0)$. 若 $\triangle P M N$ 为等边三角形, 且 $\left|P F_2\right|=\left|F_2 M\right|=\left|F_2 N\right|$, 则双曲线 $C$ 的浙近线方程为
$\text{A.}$ $y= \pm \frac{2 \sqrt{2}}{3} x$
$\text{B.}$ $y= \pm \frac{\sqrt{5}}{3} x$
$\text{C.}$ $y= \pm x$
$\text{D.}$ $y= \pm \frac{\sqrt{7}}{3} x$
多选题 (共 4 题 ),每题有多个选项正确
已知在边长为 2 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, 点 $M$ 在线段 $B_1 D_1$ 上 (含端点位置), 现有如下说法: (1) $C M / /$ 平面 $A_1 B D$; (2) $C M \perp A C_1$; (3) 点 $M$ 到平面 $A B C_1 D_1$ 的距离的最大值为 $1 ;(4) \triangle A_1 B D$ 为等边三角形. 则正确的说法个数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
已知正数 $a, b, c$ 满足 $a, b, c \neq 1, a < b < c$, 且 $a+b=c$, 记 $m=\log _c\left(a^x+b^x\right), n=\log _b\left(c^x-a^x\right)$, 则下列说法 正确的是
$\text{A.}$ 若 $a, b, c \in(1,+\infty)$, 则 $\forall x \in(1,+\infty)$, 都有 $m < n < x$
$\text{B.}$ 若 $a, b, c \in(1,+\infty)$, 则 $\forall x \in(0,1)$, 都有 $n < x < m$
$\text{C.}$ 若 $a, b, c \in(1,+\infty)$, 则 $\forall x \in(0,+\infty)$, 都有 $|m-x| \leqslant|n-x| \leqslant|m-n|$
$\text{D.}$ 若 $a, b, c \in(0,1)$, 则 $\forall x \in[1,+\infty)$, 都有 $|n-x| \leqslant|m-x| \leqslant|m-n|$
已知函数 $f(x)=\sin \left(x-\frac{\pi}{4}\right) \cdot|\sin x+\cos x|$, 则下列说法正确的是
$\text{A.}$ 函数 $f(x)$ 的最小正周期为 $2 \pi$
$\text{B.}$ 函数 $f(x)$ 在 $\left[\frac{\pi}{2}, \frac{3 \pi}{4}\right]$ 上单调递減
$\text{C.}$ 若 $f\left(x_1\right)+f\left(x_2\right)=-\sqrt{2}$, 则 $x_1+x_2$ 的值可以是 $\frac{3 \pi}{2}$
$\text{D.}$ 函数 $g(x)=4 f(x)-x$ 有 4 个零点
已知 $\lambda>0$, 若关于 $x$ 的方程 $\frac{\mathrm{e}^{x-1}}{x}-\lambda x+\lambda \ln (\lambda x)=0$ 存在正零点, 则实数 $\lambda$ 的值可能为
$\text{A.}$ $\frac{1}{\mathrm{e}}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\mathrm{e}$
$\text{D.}$ 2
填空题 (共 4 题 ),请把答案直接填写在答题纸上
为了反映城市的人口数量 $x$ 与就业压力指数 $y$ 之间的变量关系, 研究人员选择使用非线性回归模型 $y=\mathrm{e}^{-\frac{9}{10}} \cdot \mathrm{e}^{\frac{7}{10} x}$ 对所测数据进行拟合, 并设 $z=\ln y$, 得到的数据如表所示, 则 $c=$
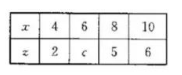
若 $3^q+\lambda \cdot 3^{-q} \geqslant 3$, 则当 $\lambda$ 取得最小值时, $q=$
阿基米德在他的著作《关于圆锥体和球体》中计算了一个椭圆的面积. 当我们垂直地缩小一个圆时, 我们得到一个椭圆. 椭圆的面积等于圆周率 $\pi$ 与椭圆的长半轴长与短半轴长的乘积. 已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
$(a>b>0)$ 的面积为 $21 \pi$, 点 $P$ 在椭圆 $C$ 上, 且点 $P$ 与椭圆 $C$ 左、生顶点连线的斜率之积为 $-\frac{9}{49}$, 记椭圆 $C$ 的两个焦点分别为 $F_1, F_2$, 则 $\left|P F_1\right|$ 的值可能为 . (横线上写出满足条件的一个值)
已知在四面体 $A B C D$ 中, $A B=A C=B C=B D=C D=\frac{2 \sqrt{3}}{3} A D=2$, 点 $E$ 在 $\triangle A B C$ 内运动 (含边界位置), 记平面 $A B C$ 与平面 $B C D$ 所成的角为 $\alpha$, 若 $4 S_{\triangle A D E} \cdot \sin \alpha=3 S_{\triangle K C E} \cdot \sin \angle D A E$, 则 $S_{\triangle M E E}$ 的最大值为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知在 $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c$, 其中 $\tan 2 C=\frac{3}{4}, C$ 为钝角, 且 $\frac{b}{a} \cos A=2 \cos B$.
(1) 求角 $B$ 的大小;
(2)若 $\triangle A B C$ 的面积为 6 , 求 $\triangle A B C$ 的周长.
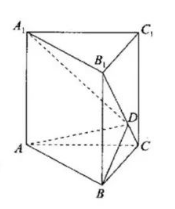
已知直三棱柱 $A B C-A_1 B_1 C_1$ 如图所示, 其中 $\angle C A B=45^{\circ}, C A=A A_1=\frac{\sqrt{2}}{2} A B$, 点 $D$ 在线段 $B_1 C$ 上 (不含端点位置).
(1) 若 $B_1 D=2 C D=2 \sqrt{2}$, 求点 $A_1$ 到平面 $A B D$ 的距离;
(2) 若平润 $A B D$ 与平面 $A B C$ 夹角的余弦值为 $\frac{1}{3}$, 求直线 $A_1 D$ 与平面 $A B D$ 所 成角的正弦值.
在数学研究性学习课程上, 老师和班级同学玩了一个游戏. 老师事先准备 3 张一模一样的卡片, 编号为 $1 、 2 、 3$ 后, 放人一个不透明的袋子中, 再准备若干枚 1 元硬币与 5 角硬币和一个储蓄罐; 然后邀请同学从袋 子中有放回地抽取 1 张卡片, 若抽到的卡片编号为 1 或 2 , 则将 1 枚 1 元硬币放入储蓄罐中, 若抽到的卡片编 号为 3 , 则将 2 枚 5 角硬币放入储蓄罐中, 如此重复 $k$ 次试验后, 记储蓄罐中的硬币总数量为 $S_k$.
(1) 若 $k=4$, 求 $S_k>5$ 的概率;
(2) 若 $k=5$, 记第 $n(n=1,2,3,4,5)$ 次抽卡且放置硬币后, 5 角硬币的数量为 $X_n, 1$ 元硬币的数量为 $Y_n$, 求在 $S_5 \geqslant 7$ 的条件下 $X_n=Y_n$ 的概率.
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $a_n=\frac{S_n+1}{2}$, 首项为 1 的正项数列 $\left\{b_n\right\}$ 满足 $b_1 \cdot b_2 \cdot b_3 \cdots \cdot b_n=$ $\left(a_n \cdot b_m\right)^n$.
(1) 求数列 $\left\{a_n\right\},\left\{b_n\right\}$ 的通项公式;
(2) 求数列 $\left\{(2 n-1) b_n\right\}$ 的前 $n$ 项和 $T_n$.
已知圆 $C_1$ 过点 $(-3,0),(-1,2),(1,0)$, 抛物线 $C_2: y^2=2 p x(p>0)$ 过点 $A\left(\frac{1}{4}, 1\right)$.
(1) 求圆 $C_1$ 的方程以及抛物线 $C_2$ 的方程;
(2) 过点 $A$ 作抛物线 $C_2$ 的切线 $l$ 与圆 $C_1$ 交于 $P, Q$ 两点, 点 $B$ 在圆 $C_1$ 上, 且直线 $B P, B Q$ 均为抛物线 $C_2$的切线, 求满足条件的所有点 $B$ 的坐标.
已知函数 $f(x)=\mathrm{e}^x-a x^2$.
(1) 若函数 $f(x)$ 在 $[1,3]$ 上有两个零点, 求实数 $a$ 的取值范围.
(2)探究: 是否存在正数 $a$, 使得 $F(x)=f(x)+a \sin x-(1+a) x$ 在 $\mathbf{R}$ 上单调递增, 若存在, 求出 $a$ 的 值; 若不存在, 请说明理由.