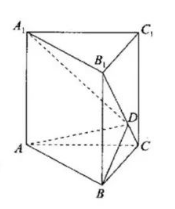
已知直三棱柱 $A B C-A_1 B_1 C_1$ 如图所示, 其中 $\angle C A B=45^{\circ}, C A=A A_1=\frac{\sqrt{2}}{2} A B$, 点 $D$ 在线段 $B_1 C$ 上 (不含端点位置).
(1) 若 $B_1 D=2 C D=2 \sqrt{2}$, 求点 $A_1$ 到平面 $A B D$ 的距离;
(2) 若平润 $A B D$ 与平面 $A B C$ 夹角的余弦值为 $\frac{1}{3}$, 求直线 $A_1 D$ 与平面 $A B D$ 所 成角的正弦值.
(1) 若 $B_1 D=2 C D=2 \sqrt{2}$, 求点 $A_1$ 到平面 $A B D$ 的距离;
(2) 若平润 $A B D$ 与平面 $A B C$ 夹角的余弦值为 $\frac{1}{3}$, 求直线 $A_1 D$ 与平面 $A B D$ 所 成角的正弦值.
