单选题 （共 12 题 ），每题只有一个选项正确
已知集合 $A=\left\{x \mid x^{2}-2 x-3 \geqslant 0\right\}, B=\{x \mid-2 \leqslant x < 2\}$, 则 $A \cap B=$
$\text{A.}$ $[1,2)$
$\text{B.}$ $[-1,1]$
$\text{C.}$ $[-1,2)$
$\text{D.}$ $[-2,-1]$
$\frac{(1+i)^{3}}{(1-i)^{2}}=(\quad)$
$\text{A.}$ $1+\mathrm{i}$
$\text{B.}$ $1-\mathrm{i}$
$\text{C.}$ $-1+\mathrm{i}$
$\text{D.}$ $-1-\mathrm{i}$
设函数 $\mathrm{f}(\mathrm{x}), \mathrm{g}(\mathrm{x})$ 的定义域都为 $\mathrm{R}$, 且 $\mathrm{f}(\mathrm{x})$ 是奇函数, $\mathrm{g}(\mathrm{x})$ 是偶函数, 则下列结论正确的是（）
$\text{A.}$ $f(x) \cdot g(x)$ 是偶函数
$\text{B.}$ $|f(x)| \cdot g(x)$ 是奇函数
$\text{C.}$ $f(x) \cdot|g(x)|$ 是奇函数
$\text{D.}$ $|f(x) \cdot g(x)|$ 是奇函数
已知 $F$ 为双曲线 $C: x^{2}-m y^{2}=3 m(m>0)$ 的一个焦点, 则点 $F$ 到 $C$ 的一条渐近线的距离为（）
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ 3
$\text{C.}$ $\sqrt{3} \mathrm{~m}$
$\text{D.}$ $3 m$
4 位同学各自在周六、周日两天中任选一天参加公益活动, 则周六、 周日都有同学参加公益活动的概率为（）
$\text{A.}$ $\frac{1}{8}$
$\text{B.}$ $\frac{3}{8}$
$\text{C.}$ $\frac{5}{8}$
$\text{D.}$ $\frac{7}{8}$
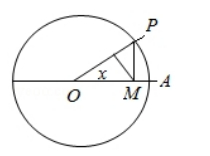
如图, 圆 $O$ 的半径为 $1, A$ 是圆上的定点, $P$ 是圆上的动点, 角 $x$ 的 始边为射线 $O A$, 终边为射线 $O P$, 过点 $P$ 作直线 $O A$ 的垂线, 垂足为 $M$, 将点 $M$ 到直线 OP 的距离表示为 $x$ 的函数 $f(x)$, 则 $y=f(x)$ 在 $[0, \pi]$ 的图象大致 为 ( )
$\text{A.}$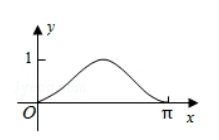 
$\text{B.}$ 
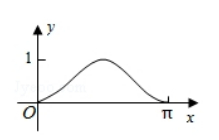$\text{C.}$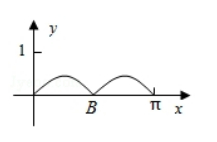 
执行如图的程序框图, 若输入的 $a, b, k$ 分别为 $1,2,3$, 则输出的
$$M=(\quad)$$
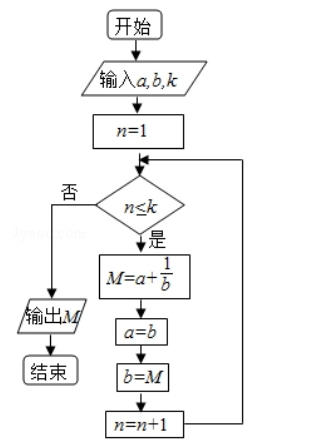
$\text{A.}$ $\frac{20}{3}$
$\text{B.}$ $\frac{7}{2}$
$\text{C.}$ $\frac{16}{5}$
$\text{D.}$ $\frac{15}{8}$
设 $\alpha \in\left(0, \frac{\pi}{2}\right), \beta \in\left(0, \frac{\pi}{2}\right)$, 且 $\tan \alpha=\frac{1+\sin \beta}{\cos \beta}$, 则（ ）
$\text{A.}$ $3 \alpha-\beta=\frac{\pi}{2}$
$\text{B.}$ $3 \alpha+\beta=\frac{\pi}{2}$
$\text{C.}$ $2 \alpha-\beta=\frac{\pi}{2}$
$\text{D.}$ $2 \alpha+\beta=\frac{\pi}{2}$
不等式组 $\left\{\begin{array}{l}x+y \geqslant 1 \\ x-2 y \leqslant 4\end{array}\right.$ 的解集记为 $D$, 有下列四个命题: $p_{1}: \forall(x, y) \in D, x+2 y \geqslant-2 p_{2}: \exists(x, y) \in D, x+2 y \geqslant 2$
$p_{3}: \forall(x, y) \in D, x+2 y \leqslant 3 p_{4}: \exists(x, y) \in D, x+2 y \leqslant-1$
其中真命题是（）
$\text{A.}$ $\mathrm{p}_{2}, \mathrm{p}_{3}$
$\text{B.}$ $\mathrm{p}_{1}, \mathrm{p}_{4}$
$\text{C.}$ $\mathrm{p}_{1}, \mathrm{p}_{2}$
$\text{D.}$ $\mathrm{p}_{1}, \mathrm{p}_{3}$
已知抛物线 $C: y^{2}=8 x$ 的焦点为 $F$, 准线为 $I, P$ 是 $I$ 上一点, $Q$ 是直 线 $P F$ 与 $C$ 的一个交点, 若 $\overrightarrow{F P}=4 \overrightarrow{F Q}$, 则 $|Q F|=(\quad)$
$\text{A.}$ $\frac{7}{2}$
$\text{B.}$ 3
$\text{C.}$ $\frac{5}{2}$
$\text{D.}$ 2
已知函数 $f(x)=a x^{3}-3 x^{2}+1$, 若 $f(x)$ 存在唯一的零点 $x_{0}$, 且 $x_{0}>$
0, 则实数 a 的取值范围是（）
$\text{A.}$ $(1,+\infty)$
$\text{B.}$ $(2,+\infty)$
$\text{C.}$ $(-\infty,-1)$
$\text{D.}$ $(-\infty,-2)$
如图, 网格纸上小正方形的边长为 1, 粗实线画出的是某多面体的 三视图, 则该多面体的各条棱中, 最长的棱的长度为（）
$\text{A.}$ $6 \sqrt{2}$
$\text{B.}$ 6
$\text{C.}$ $4 \sqrt{2}$
$\text{D.}$ 4
填空题 （共 12 题 ），请把答案直接填写在答题纸上
$(\mathrm{x}-\mathrm{y})(\mathrm{x}+\mathrm{y})^{8}$ 的展开式中 $\mathrm{x}^{2} \mathrm{y}^{7}$ 的系数为
甲、乙、丙三位同学被问到是否去过 A, B, C三个城市时, 甲说: 我去过的城市比乙多, 但没去过 $B$ 城市;
乙说：我没去过 C 城市;
丙说: 我们三人去过同一城市;
由此可判断乙去过的城市为 （ ）
已知 $\mathrm{A}, \mathrm{B}, \mathrm{C}$ 为圆 $\mathrm{O}$ 上的三点, 若 $\overrightarrow{\mathrm{AO}}=\frac{1}{2}(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}})$, 则 $\overrightarrow{\mathrm{AB}}$ 与 $\overrightarrow{\mathrm{AC}}$ 的 夹角为
已知 $a, b, c$ 分别为 $\triangle A B C$ 的三个内角 $A, B, C$ 的对边, $a=2$ 且 ( $2+b$ ) $(\sin A-\sin B)=(c-b) \sin C$, 则 $\triangle A B C$ 面积的最大值为 （ ）
已知数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}, a_{1}=1, a_{n} \neq 0, a_{n} a_{n+1}=\lambda S_{n}-1$, 其中$\lambda$ 为常数.
(I ) 证明: $a_{n+2}-a_{n}=\lambda$
(II）是否存在 $\lambda$, 使得 $\left\{a_{n}\right\}$ 为等差数列? 并说明理由.
从某企业生产的某种产品中抽取 500 件, 测量这些产品的一项质 量指标值, 由测量结果得如下频率分布直方图:
(I) 求这 500 件产品质量指标值的样本平均数 $\mathrm{x}$ 和样本方差 $\mathrm{s}^{2}$ (同一组中数据 用该组区间的中点值作代表）;
（II）由直方图可以认为, 这种产品的质量指标值 Z 服从正态分布 $\mathrm{N}\left(\mu, \sigma^{2}\right)$, 其中 $\mu$ 近似为样本平均数 $\mathrm{x}, \sigma^{2}$ 近似为样本方差 $s^{2}$.
(i) 利用该正态分布, 求 $P(187.8 < Z < 212.2)$;
（ii）某用户从该企业购买了 100 件这种产品, 记 X表示这 100 件产品中质量指 标值位于区间 $(187.8,212.2 ）$ 的产品件数, 利用（i）的结果, 求 EX. 附: $\sqrt{150} \approx 12.2$.
若 $Z \sim N\left(\mu, \sigma^{2}\right)$ 则 $P(\mu-\sigma < Z < \mu+\sigma)=0.6826, P(\mu-2 \sigma < Z < \mu+2 \sigma)=0.9544$
如图, 三棱柱 $\mathrm{ABC}-\mathrm{A}_{1} \mathrm{~B}_{1} \mathrm{C}_{1}$ 中, 侧面 $\mathrm{BB}_{1} \mathrm{C}_{1} \mathrm{C}$ 为菱形, $\mathrm{AB} \perp \mathrm{B}_{1} \mathrm{C}$.
(I) 证明: $\mathrm{AC}=\mathrm{AB}_{1}$;
(II ) 若 $\mathrm{AC} \perp \mathrm{AB}_{1}, \angle \mathrm{CBB}_{1}=60^{\circ}, \mathrm{AB}=\mathrm{BC}$, 求二面角 $\mathrm{A}-\mathrm{A}_{1} \mathrm{~B}_{1}-\mathrm{C}_{1}$ 的余弦值.
已知点 $A(0,-2)$, 椭圆 $E: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 的离心率为 $\frac{\sqrt{3}}{2}$
, $\mathrm{F}$ 是椭圆的右焦点, 直线 $\mathrm{AF}$ 的斜率为 $\frac{2 \sqrt{3}}{3}, \mathrm{O}$ 为坐标原点.
(I) 求 $\mathrm{E}$ 的方程;
（II ) 设过点 $\mathrm{A}$ 的直线 $\mathrm{I}$ 与 $\mathrm{E}$ 相交于 $\mathrm{P}, \mathrm{Q}$ 两点, 当 $\triangle \mathrm{OPQ}$ 的面积最大时, 求 I 的方程.
设函数 $f(x)=a e^{x} \ln x+\frac{b e^{x-1}}{x}$, 曲线 $y=f(x)$ 在点 (1, $f(1 ）$ 处 得切线方程为 $y=e(x-1)+2$.
(I) 求 $a 、 b$;
(II ) 证明: $f(x)>1$.
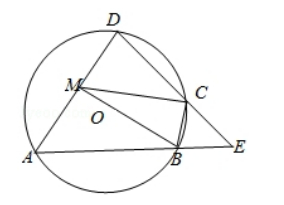
如图, 四边形 $A B C D$ 是 $\odot O$ 的内接四边形, $A B$ 的延长线与 $D C$ 的延 长线交于点 $E$, 且 $C B=C E$.
(I) 证明: $\angle \mathrm{D}=\angle \mathrm{E}$;
(II) 设 $A D$ 不是 $\odot O$ 的直径, $A D$ 的中点为 $M$, 且 $M B=M C$, 证明: $\triangle A D E$ 为等 边三角形.
已知曲线 $C: \frac{x^{2}}{4}+\frac{y^{2}}{9}=1$, 直线 I: $\left\{\begin{array}{l}x=2+t \\ y=2-2 t\end{array}\right.$ (t为参数)
( I ) 写出曲线 C 的参数方程, 直线 I 的普通方程.
(II ) 过曲线 C 上任意一点 $P$ 作与 I 夹角为 $30^{\circ}$ 的直线, 交 $I$ 于点 $A$, 求 $|P A|$ 的最 大值与最小值.
24. 若 $a>0, b>0$, 且 $\frac{1}{a}+\frac{1}{b}=\sqrt{a b}$.
(I) 求 $a^{3}+b^{3}$ 的最小值;
(II) 是否存在 $a, b$, 使得 $2 a+3 b=6$ ? 并说明理由.