如图, 四边形 $A B C D$ 是 $\odot O$ 的内接四边形, $A B$ 的延长线与 $D C$ 的延 长线交于点 $E$, 且 $C B=C E$.
(I) 证明: $\angle \mathrm{D}=\angle \mathrm{E}$;
(II) 设 $A D$ 不是 $\odot O$ 的直径, $A D$ 的中点为 $M$, 且 $M B=M C$, 证明: $\triangle A D E$ 为等 边三角形.
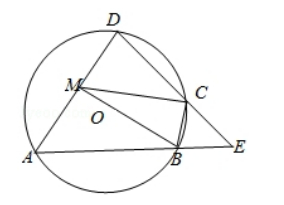
(I) 证明: $\angle \mathrm{D}=\angle \mathrm{E}$;
(II) 设 $A D$ 不是 $\odot O$ 的直径, $A D$ 的中点为 $M$, 且 $M B=M C$, 证明: $\triangle A D E$ 为等 边三角形.
