单选题 (共 21 题 ),每题只有一个选项正确
华罗庚说过: “数形结合百般好, 隔裂分家万事非. ”请运用这句话中提到的思想方法 判断方程 $\frac{1}{x}+2=-x^2+4 x$ 的根的情况是
$\text{A.}$ 有三个实数根
$\text{B.}$ 有两个实数根
$\text{C.}$ 有一个实数根
$\text{D.}$ 无实数 根
如图, $\triangle A B C$ 中, $\angle A B C=45^{\circ}, B C=4, \tan \angle A C B=3, A D \perp B C$ 于 $D$, 若将 $\triangle A D C$ 绕点 $D$ 逆时针方 向旋转得到 $\triangle F D E$, 当点 $E$ 恰好落在 $A C$ 上, 连接 $A F$. 则 $A F$ 的长为

$\text{A.}$ $\frac{3}{5} \sqrt{10}$
$\text{B.}$ $\frac{3}{10} \sqrt{10}$
$\text{C.}$ $\sqrt{10}$
$\text{D.}$ $2$
“如果二次函数 $y=a x^2+b x+c$ 的图象与 $x$ 轴有两个公共点, 那么一元二次方程 $a x^2+b x+c=0$ 有 两个不相等的实数根.” 请根据你对这句话的理解, 解决下面问题: 若 $m 、 n(m < n)$ 是关于 $x$ 的方程 $1-(x-a)(x-b)=0$ 的两根, 且 $a < b$, 则 $a 、 b 、 m 、 n$ 的大小关系是
$\text{A.}$ $m < a < b < n$
$\text{B.}$ $a < m < n < b$
$\text{C.}$ $a < m < b < n$
$\text{D.}$ $m < a < n < b$
如图, 若方格纸中每个小正方形的边长均为 1 , 则阴影部分的面积为
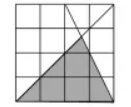
$\text{A.}$ 5
$\text{B.}$ 6
$\text{C.}$ $\frac{16}{3}$
$\text{D.}$ $\frac{17}{3}$
函数 $y=|x+1|-2$, 当 $m \leq x \leq 4$, 对应 $y$ 的取值范围为 $-2 \leq y \leq 3$, 则 $m$ 的取值范围 为
$\text{A.}$ $m=-1$
$\text{B.}$ $m \leq-1$
$\text{C.}$ $-6 \leq m \leq-1$
$\text{D.}$ $-1 \leq m < 4$
如图, 四边形 $A B C D$ 的顶点都在坐标轴上, 若 $A B / / C D, \triangle A O B$ 与 $\triangle C O D$ 的面积分 别为 8 和 18 , 若双曲线 $y=\frac{k}{x}$ 恰好经过 $B C$ 的中点 $E$, 则 $k$ 的值为

$\text{A.}$ 3
$\text{B.}$ -3
$\text{C.}$ 6
$\text{D.}$ -6
如图, 在平行四边形 $A B C D$ 中, 点 $E 、 F 、 G$ 分别是 $A D 、 B C 、 C D$ 的中点, $B E \perp E G, A D=2 \sqrt{5}, A B=3$, 则 $A F$ 的长是
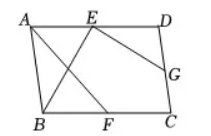
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
小英、小亮、小明和小华四名同学参加了“学用杯”竞赛选拔赛, 小亮和小华两个同 学的得分和等于小明和小英的得分和; 小英与小亮的得分和大于小明和小华的得分和, 小华的得分超过小明与小亮的得分和. 则这四位同学的得分由大到小的顺序是
$\text{A.}$ 小明, 小亮, 小华, 小英
$\text{B.}$ 小华, 小明, 小亮, 小英
$\text{C.}$ 小英, 小华, 小亮, 小明
$\text{D.}$ 小亮, 小英, 小华, 小明
如图, 抛物线 $y=a x^2+b x+c(a \neq 0)$ 的对称轴为 $x=-1$, 与 $x$ 轴的一个交点在 $(-3,0)$ 和 $(-2,0)$ 之间, 其部分图象如图所示, 则下列结论:
(1) $b^2-4 a c>0 $
(2) $2 a=b$
(3) 点 $\left(-\frac{7}{2}, y_1\right) 、\left(-\frac{3}{2}, y_2\right) 、\left(\frac{5}{4}, y_2\right)$ 是该抛物线上的点, 则 $y_1 < y_2 < y_2$;
(4) $3 b+2 c < 0 $
(5) $t(a t+b) \leq a-b$ ( $t$ 为任意实数);
(6) $(a+c)^2>b^2$, 其中正确结论 的个数是
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
如图, 分别以正方形 $A B C D$ 的两条边 $A D 、 C D$ 为边向外作两个正三角形, 即 $\triangle A D G$ 与 $\triangle C$ $D F$, 然后延长 $G A, F C$ 交于点 $E$, 得到一个 “镖型” $A B C E$. 已知正方形 $A B C D$ 的边长为 2 , 则 “镖 型” $A B C E$ 的周长为
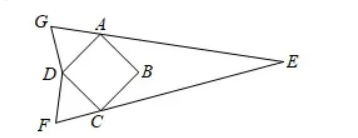
$\text{A.}$ $8+\sqrt{10}$
$\text{B.}$ $4+4 \sqrt{5}$
$\text{C.}$ $4+4 \sqrt{3}$
$\text{D.}$ $8+4 \sqrt{3}$
如图所示的是由一些火柴棒摆成的图䋈: 摆第 1 个图案用了 5 拫火柴, 摆第 2 个图案用了9 根火柴, 摆第 3 个图案用了 13 根火柴.....按照这种方式摆下去, 摆第 10 个图案需要用的火柴棒根数是
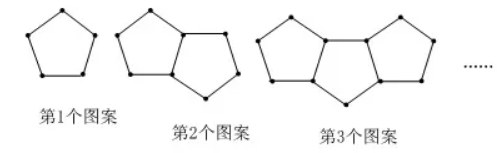
$\text{A.}$ 39
$\text{B.}$ 40
$\text{C.}$ 41
$\text{D.}$ 42
如果关于 $x$ 的不等式组 $ \left\{\begin{array}{l}
\frac{x-m}{2} \geq 0 \\
x+3 < 3(x-1)
\end{array}\right.$ 的解集为 $x>3$, 且关于 $y$ 的分式方程 $\frac{3-y}{2-y}+\frac{m}{y-2}=3$ 有非负整数解, 则符合条件的整数 $m$ 的值的和是
$\text{A.}$ -4
$\text{B.}$ -3
$\text{C.}$ -1
$\text{D.}$ -7
数学是研究化学的重要工具, 数学知识广泛应用于化学邻域, 比如在学习化学的醇类化 学式中, 甲醇化学式为 $\mathrm{CH}_3 \mathrm{OH}$, 乙䤃化学式为 $\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}$, 丙醇化学式为 $\mathrm{C}_3 \mathrm{H}_7 \mathrm{OH}$..., 设碳原子 的数目为 $n$ ( $n$ 为正整数), 则醇类的化学式可以用下列哪个式子来表示
$\text{A.}$ $\mathrm{C}_n \mathrm{H}_{3 n} \mathrm{OH}$
$\text{B.}$ $\mathrm{C}_n \mathrm{H}_{2 n-1} \mathrm{OH}$
$\text{C.}$ $\mathrm{C}_n \mathrm{H}_{2 n}+{ }_1 \mathrm{OH}$
$\text{D.}$ $\mathrm{C}_n \mathrm{H}_{2 \mathrm{n}} \mathrm{OH}$
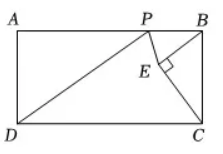
如图, 已知矩形 $A B C D, A B=8, A D=4$, 点 $E$ 是矩形内部 一动点, 且 $\angle B E C=90^{\circ}$, 点 $P$ 是 $A B$ 边上一动点, 连接 $P D, P E$, 则$P D+P E$ 长度的最小值为
$\text{A.}$ 8
$\text{B.}$ $4 \sqrt{5}$
$\text{C.}$ 10
$\text{D.}$ $4 \sqrt{5}-2$
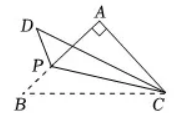
如图所示, 腰长为 2 的等腰Rt $\triangle A B C$ 中, $\angle A=90^{\circ}, P$ 为腰 $A B$ 上 的一个动点, 将 $\triangle P B C$ 沿 $C P$ 折桑得对应 $\triangle P D C$, 当 $P D$ 与 $\triangle A B C$ 的某一条边垂直时, $P D$ 的长为
$\text{A.}$ 2 或 $4-2 \sqrt{2}$
$\text{B.}$ 2 或 $4+2 \sqrt{2}$
$\text{C.}$ 4或 $4-2 \sqrt{2}$
$\text{D.}$ 4或 $4+2 \sqrt{2}$
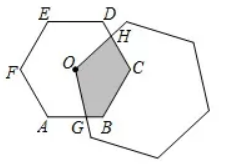
一个适当大的正六边形, 它的一个顶点与一个边长为定值 的小正六边形 $A B C D E F$ 的中心 $O$ 重合, 且与边 $A B 、 C D$ 相交于 $G$ 、$H$ (如图). 图中阴影部分的面积记为 $S$ ,三条线段 $G B 、 B C 、 C H$ 的长度之和记为 $l$,
在大正六边形绕於旋转过程中, 下列说法正确的是
$\text{A.}$ $S$ 变化,$l$不变
$\text{B.}$ $S$不变,$l$变化
$\text{C.}$ $S$ 变化, $l$变化
$\text{D.}$ $S$ 与$l$均不变
已知二次函数 $y=m x^2-4 m x$ ( $m$ 为不等于 0 的常数), 当 $-2 \leq x \leq 3$ 时, 函数 $y$ 的最小值为 -2 , 则$m$的值为
$\text{A.}$ $\pm \frac{1}{6}$
$\text{B.}$ $-\frac{1}{6}$ 或 $\frac{1}{2}$
$\text{C.}$ $-\frac{1}{6}$ 或 $\frac{2}{3}$
$\text{D.}$ $\frac{1}{6}$ 或2
若抛物线 $M: y=x^2+(3 m-1) x-5$ 与抛物线 $M^{\prime}: y=x^2-6 x-n+1$ 关于直线 $x=1$ 对称, 则 $m, n$ 的值分别为
$\text{A.}$ $m=-\frac{11}{3}, n=-2$
$\text{B.}$ $m=\frac{1}{3}, n=-2$
$\text{C.}$ $m=\frac{1}{3}, n=2$
$\text{D.}$ $m=1, n=-2$
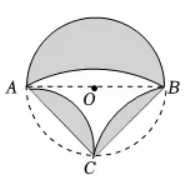
如图, 在 $\odot O$ 中, $A B$ 为直径, 点 $C$ 是圆上一点, 连接 $A C, B C$, 以 $C$ 为圆心, $A C$ 的长为半径作弧, 恰好经过点 $B$, 将 $\odot O$ 分别沿 $A C$, $B C$ 向内翻折若 $A B=4$, 则图中阴影部分的面积是
$\text{A.}$ $4 \pi-2$
$\text{B.}$ $16 \pi-2$
$\text{C.}$ $2 \pi$
$\text{D.}$ $14 \pi$