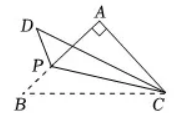
如图所示, 腰长为 2 的等腰Rt $\triangle A B C$ 中, $\angle A=90^{\circ}, P$ 为腰 $A B$ 上 的一个动点, 将 $\triangle P B C$ 沿 $C P$ 折桑得对应 $\triangle P D C$, 当 $P D$ 与 $\triangle A B C$ 的某一条边垂直时, $P D$ 的长为
A
2 或 $4-2 \sqrt{2}$
B
2 或 $4+2 \sqrt{2}$
C
4或 $4-2 \sqrt{2}$
D
4或 $4+2 \sqrt{2}$
E
F