单选题 (共 12 题 ),每题只有一个选项正确
已知全集 $U=\{1,2,3,4,5,6\}$, 集合 $M=\{1,3,6\}, N=\{2,3,4\}$, 则 $\complement_U(M \cup N)=$
$\text{A.}$ $|5|$
$\text{B.}$ $\{1,2\}$
$\text{C.}$ $\{3,4\}$
$\text{D.}$ $\{1,2,3,4\}$
已知 $m, n$ 为实数, $1-\mathrm{i}$ ( $\mathrm{i}$ 为虚数単位) 是关于 $x$ 的方程 $x^2-m x+n=0$ 的一个根, 则 $m+n=$
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
设数列 $\left\{a_n\right\}$ 为正项等差数列, 且其前 $n$ 項和为 $S_n$, 若 $S_{2023}=2023$, 则下列判断错误的是
$\text{A.}$ $a_{1012}=1$
$\text{B.}$ $a_{1013} \geqslant 1$
$\text{C.}$ $S_{2022}>2022$
$\text{D.}$ $S_{2024} \geqslant 2024$
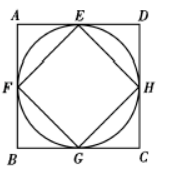
已知四边形 $A B C D$ 为正方形, 其内切圆 $I$ 与各边分别切于 $E, F, G$ $H$, 连接 $E F, F G, G H, H E$, 如图所示. 现向正方形 $A B C D$ 内随机拋烪 一枚豆子, 记事件 $M$ 为豆子落在圆 $I$ 内, 事件 $N$ 为豆子落在四边开 $E F G H$ 外, 则 $P(N \mid M)=$
$\text{A.}$ $1-\frac{\pi}{4}$
$\text{B.}$ $\frac{\pi}{4}$
$\text{C.}$ $1-\frac{2}{\pi}$
$\text{D.}$ $\frac{2}{\pi}$
已知 $D, E$ 分别是 $\triangle A B C$ 的边 $A B, A C$ 上的点, 且满足 $\overrightarrow{A D}=\frac{1}{3} \overrightarrow{A B}, \overrightarrow{A E}=\frac{2}{3} \overrightarrow{A C}$. $F$ 为直线 $D E$ 与直线 $B C$ 的交点. 若 $\overrightarrow{A F}=\lambda \overrightarrow{A B}+\mu \overrightarrow{A C}$ ( $\lambda, \mu$ 为实数), 则 $\mu-\lambda$ 的值为
$\text{A.}$ $1$
$\text{B.}$ $-\frac{5}{3}$
$\text{C.}$ $\frac{5}{3}$
$\text{D.}$ $\frac{1}{2}$
已知函数 $f(x)=2 \cos ^2 \omega x+\sqrt{3} \sin 2 \omega x-1(\omega>0)$ 的最小正周期为 $\frac{\pi}{2}$, 把函数 $f(x)$ 的图象向右平移 $\dfrac{\pi}{12}$个单位长度,得到函数$g(x)$函数,则函数$g(x)0$的函数图形的对称中心为
$\text{A.}$ $\left(-\frac{\pi}{24}, 0\right)$
$\text{B.}$ $\left(\frac{\pi}{24}, 0\right)$
$\text{C.}$ $\left(-\frac{\pi}{48}, 0\right)$
$\text{D.}$ $\left(\frac{\pi}{48}, 0\right)$
已知双曲线 $C: \frac{x^2}{a^2} - \frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1, F_2, P$ 是双曲线 $C$ 的一条渐近线上的点, 且线段 $P F_1$ 的中点 $M$ 在另一条渐近线上. 若 $\angle P F_2 F_1=45^{\circ}$, 则双曲线 $C$ 的 离心率为
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ $2$
$\text{D.}$ $\sqrt{5}$
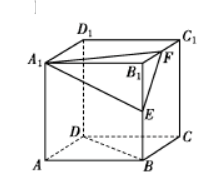
如图, 在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $E, F$ 分别是棱 $B_1 B, B_1 C_1$ 的 中点, 则过线段 $B D$ 且垂直于平面 $A_1 E F$ 的截面图形为
$\text{A.}$ 等腰梯形
$\text{B.}$ 三角形
$\text{C.}$ 正方形
$\text{D.}$ 矩形
某中学坚持“五育”并举, 全面推进素质教育. 为了更好地增强学 生们的身体素质, 校长带领同学们一起做俯卧撑煅炼.锻炼是否达到中等强度运动, 简单测量方法为 $f(t)=k \mathrm{e}^{t}$, 其中 $t$ 为运动后心率 (单位: 次/分) 与正常时心率的比值, $k$ 为每个个体的体质健康系数. 若 $f(t)$ 介于 $[28,34]$ 之间, 则达到了中等强度运动; 若低于 28 , 则运动不足; 若高于34 , 则运动过量. 已知某同学正常时心率为80 , 体质健康系数 $k=7$, 经过俯卧撑后心率 $y$ (单位:次/分) 满足 $y=80\left(\ln \sqrt{\frac{x}{12}}+1\right), x$ 为俯卧撑个数. 已知俯卧撑每组 12个, 若该同学要达到中等强度运动, 则较合适的俯卧搅组数为 ( $\mathrm{e}$ 为自然对数的底 数, $\mathrm{e} \approx 2.718)$
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
设函数 $f(x)$ 的定义域为 $\mathbf{R}, f(x+1)$ 为奇函数, $f(x+2)$ 为偶函数, 当 $x \in[1,2]$ 时, $f(x)=$ $a x^2+b$. 若 $f(0)+f(3)=3$, 则 $f\left(\frac{9}{2}\right)=$
$\text{A.}$ $-\frac{5}{4}$
$\text{B.}$ $-\frac{3}{4}$
$\text{C.}$ $\frac{7}{4}$
$\text{D.}$ $\frac{5}{4}$
实数 $x, y, z$ 分别满足 $x^{2022}=\mathrm{e}, 2022^y=2023,2022 z=2023$, 则 $x, y, z$ 的大小关系为
$\text{A.}$ $x>y>z$
$\text{B.}$ $x>z>y$
$\text{C.}$ $z>x>y$
$\text{D.}$ $y>x>z$
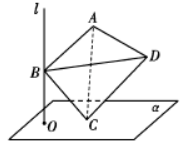
如图, 直线 $l \perp$ 平面 $\alpha$, 垂足为 $O$, 正四面体 $A B C D$ (所有棱长都 相等的三棱锥) 的棱长为 $2, C$ 在平面 $\alpha$ 内, $B$ 是直线 $l$ 上的动 点, 当 $O$ 到 $A D$ 的距离最大时, 该正四面体在平面 $\alpha$ 上的射影 面积为
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ $\sqrt{2}$
$\text{D.}$ $1+\frac{\sqrt{2}}{2}$
填空题 (共 11 题 ),请把答案直接填写在答题纸上
已知函数 $ f(x)=\left\{\begin{array}{l}
x^2+x+1, x \geqslant 0 \\
2 x+1, x < 0
\end{array}\right. $ 若 $f(m) < f(2-m^2)$, 则m的取值范围是
安排 $A, B, C, D, E$ 五名志愿者到甲,乙两个福利院做服务工作, 每个福利院至少安排一 名志愿者,则 $A, B$ 被安排在不同的福利院的概率为
已知数列 $\left\{a_n\right\}$ 满足 $a_1=0, a_{n+1}=-a_n^2+a_n+c\left(n \in \mathbf{N}^*\right)$. 若数列 $\left\{a_n\right\}$ 为单调递增数列, 则实 数 $c$ 的取值范围为
已知在 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别是 $a, b, c$, 在①$a \sin C-c \cos \left(A-\frac{\pi}{6}\right)=0$; ② $2 c \cos A=$ $a \cos B+b \cos A$; (3) $b \sin B+c \sin C-a \sin A-b \sin C=0$ 中任选一个作为条件解答下面两个问 题.
(1) 求角 $A$;
(2) 已知 $b=6, S_{\triangle A B C}=3 \sqrt{3}$, 求 $a$ 的值.
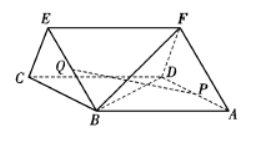
如图, 在三棱柱 $A D F-B C E$ 中, 四边形 $A B C D$ 是菱形, $\angle A B C=120^{\circ}, A F=\sqrt{3}, A D=2 D F=2, P, Q$ 分别为 $A D, B E$ 的中点, 且平面 $A D F \perp$ 平面 $A B C D$.
(1) 求证: $D F \perp P Q$;
(2) 求直线 $P Q$ 与平面 $B D F$ 所成角的正弦值.
某学校筹备成立足球社团,由于报名人数太多, 需对报名者进行“点球测试” 来决定是否 录取. 规则如下: 每人最多有四次机会, 只要连续踢进 2 个点球, 则停止踢球并予以录 取,若已经确定不能连续踢进 2 个点球,则停止踢球且不予录取. 下表是呆同学六次训 练数据, 以这 150 个点球中的进球频率代表其单次点球踢进的概率.

(1)求该同学被录取的概率;
(2)若该同学要进行 “点球测试”, 记他在测试中进球的个数为 $X$, 求随机变量 $X$ 的期 望.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的有焦点 $F(1,0)$, 点 $M\left(\frac{\sqrt{6}}{2}, \frac{1}{2}\right)$ 在椭圆 $C$ 上.
(1) 求椭圆 $C$ 的标准方程;
(2) 过点 $P(2,1)$ 的直线 $l$ 与椭圆 $C$ 交于 $A, B$ 两点. 若 $\overrightarrow{P A}=\lambda \overrightarrow{P B}, \overrightarrow{A Q}=\lambda \overrightarrow{Q B}(\lambda>0)$, 求 $|\overrightarrow{O Q}|$ 的最小值 ( $O$ 是坐标原点).
已知函数 $f(x)=1 \frac{a x^3}{\mathrm{e}^x}(a \neq 0)$.
(1) 讨论 $f(x)$ 在 $(0,+\infty)$ 上的单调性;
(2) 若不等式 $2 \mathrm{e}^x f(x) \geqslant x^3 \ln x+x^2+3 x$ 晅成立, 求实数 $a$ 的取值范邦.
在直角坐标系 $x O y$ 中, 曲线 $C_1$ 的参数方程为 $\left\{\begin{array}{l}x=2 \cos \varphi, \\ y=\sqrt{2} \sin \varphi\end{array}\right.$ (其中 $\varphi$ 为参数), 以 $O$ 为极点, $x$ 轴的正半轴为极轴建立极坐标系, 曲线 $C_2$ 的极坐标方程为 $\rho \cos ^2 \theta+4 \cos \theta-\rho=0$.
(1) 求曲线 $C_1$ 的普通方程和曲线 $C_2$ 的直角坐标方程;
(2) 射线 $l: \theta=\alpha$ 与曲线 $C_1, C_2$ 分别交于点 $A, B$ (均异于极点), 当 $\frac{\pi}{4} \leqslant \alpha \leqslant \frac{\pi}{3}$ 时, 求 $\frac{|O B|}{|O A|}$ 的最小值.
已知正实数 $a, b, c$ 满足 $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$.
(1) 求 $a+4 b+9 c$ 的最小值;
(2) 证明: $\frac{b+c}{\sqrt{a}}+\frac{a+c}{\sqrt{b}}+\frac{a+b}{\sqrt{c}} \geqslant 2 \sqrt{a b c}$.