单选题 (共 12 题 ),每题只有一个选项正确
下列各数中, 最小的数是
$\text{A.}$ $-3$
$\text{B.}$ $0$
$\text{C.}$ $1$
$\text{D.}$ $2$
下列图形是轴对称图形的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
在今年举行的第 127 届“广交会”上, 有近 26000 家厂家进行“云端销售”. 其中数据 26000 用科学记数法表示 为
$\text{A.}$ $26 \times 10^3$
$\text{B.}$ $2.6 \times 10^3$
$\text{C.}$ $2.6 \times 10^4$
$\text{D.}$ $0.26 \times 10^5$
把黑色三角形按如图所示的规律拼图案, 其中第(1)个图案中有 1 个黑色三角形, 第(2)个图案中有 3 个黑色 三角形, 第(3)个图案中有 6 个黑色三角形, ..., 按此规律排列下去, 则第(5)个图案中黑色三角形的个数为
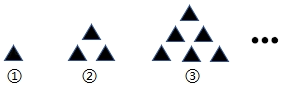
$\text{A.}$ 10
$\text{B.}$ 15
$\text{C.}$ 18
$\text{D.}$ 21
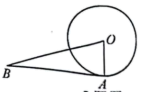
如图, $\mathrm{AB}$ 是 $O$ 的切线, $A$ 切点, 连接 $\mathrm{OA}, \mathrm{OB}$, 若 $\angle B=20^{\circ}$, 则 $\angle A O B$ 的度数为
$\text{A.}$ $40^{\circ}$
$\text{B.}$ $50^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $70^{\circ}$
下列计算中, 正确的是
$\text{A.}$ $\sqrt{2}+\sqrt{3}=\sqrt{5}$
$\text{B.}$ $2+\sqrt{2}=2 \sqrt{2}$
$\text{C.}$ $\sqrt{2} \times \sqrt{3}=\sqrt{6}$
$\text{D.}$ $2 \sqrt{3}-2=\sqrt{3}$
解一元一次方程 $\frac{1}{2}(x+1)=1-\frac{1}{3} x$ 时, 去分母正确的是
$\text{A.}$ $3(x+1)=1-2 x$
$\text{B.}$ $2(x+1)=1-3 x$
$\text{C.}$ $2(x+1)=6-3 x$
$\text{D.}$ $3(x+1)=6-2 x$
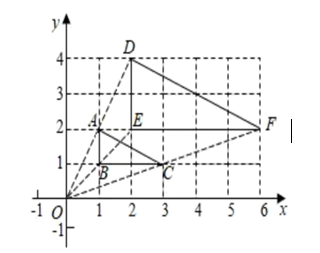
如图, 在平面直角坐标系中, $\mathrm{V} A B C$ 的顶点坐标分别是 $A(1,2), B(1,1), C(3,1)$, 以原点为位似中心, 在原点的同侧画 $\mathrm{V} D E F$, 使 $\mathrm{V} D E F$ 与 $\mathrm{V} A B C$ 成位似图形, 且相似比为 $2: 1$, 则线段 $D F$ 的长度为
$\text{A.}$ $\sqrt{5}$
$\text{B.}$ $2$
$\text{C.}$ $4$
$\text{D.}$ $2 \sqrt{5}$
如图,在距某居民楼 $A B$ 楼底 $B$ 点左侧水平距离 $60 \mathrm{~m}$ 的 $C$ 点处有一个山坡, 山坡 $\mathrm{CD}$ 的坡度 (或坡比) $i=1: 0.75$, 山坡坡底 $C$ 点到坡顶 $D$ 点的距离 $C D=45 \mathrm{~m}$, 在坡顶 $D$ 点处测得居民楼楼顶 $A$ 点的仰角为 $28^{\circ}$, 居民楼 $A B$ 与山坡 $C D$ 的剖面在同一平面内, 则居民楼 $A B$ 的高度约为
(参考数据: $\sin 28^{\circ} \approx 0.47, \cos 28^{\circ} \approx 0.88, \tan 28^{\circ} \approx 0.53$ )
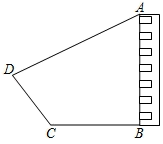
$\text{A.}$ $76.9 \mathrm{~m}$
$\text{B.}$ $82.1 \mathrm{~m}$
$\text{C.}$ $94.8 \mathrm{~m}$
$\text{D.}$ $112.6 \mathrm{~m}$
若关于 $x$ 的一元一次不等式结 $\left\{\begin{array}{l}\frac{3 x-1}{2} \leq x+3 \\ x \leq a\end{array}\right.$ 的解集为 $x \leq a$; 具关于 $y$ 的分式方程 $\frac{y-a}{y-2}+\frac{3 y-4}{y-2}=1$ 有 正整数解, 则所有满足条件的整数 $a$ 的值之积是
$\text{A.}$ $7$
$\text{B.}$ $-14$
$\text{C.}$ $28$
$\text{D.}$ $-56$
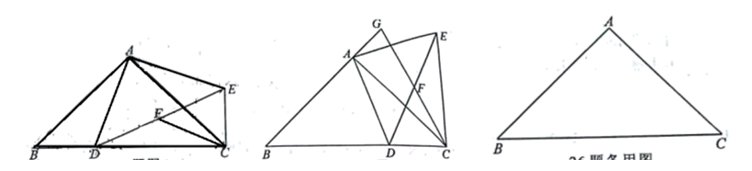
.如图, 三角形纸片 $A B C$, 点 $D$ 是 $B C$ 边上一点, 连接 $A D$, 把 $\triangle A B D$ 沿着 $A D$ 翻折, 得到 $V A E D, D E$ 与 $\mathrm{AC}$ 交于点 $G$, 连接 $B E$ 交 $A D$ 于点 $F$. 若 $D G=G E, A F=3, B F=2, \mathrm{~V} A D G$ 的面积为 2 , 则点 $F$ 到 $B C$ 的距离为
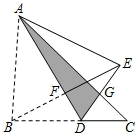
$\text{A.}$ $\frac{\sqrt{5}}{5}$
$\text{B.}$ $\frac{2 \sqrt{5}}{5}$
$\text{C.}$ $\frac{4 \sqrt{5}}{5}$
$\text{D.}$ $\frac{4 \sqrt{3}}{3}$
如图, 在平面直角坐标系中, 矩形 $A B C D$ 的对角线 $A C$ 的中点与坐标原点重合, 点 $E$ 是 $x$ 轴上一点, 连接 $\mathrm{AE}$. 若 $\mathrm{AD}$ 平分 $\angle O A E$, 反比例函数 $y=\frac{k}{x}(k>0, x>0)$ 的图象经过 $\mathrm{AE}$ 上的两点 $\mathrm{A}, \mathrm{F}$, 且 $A F=E F, \triangle A B E$ 的面积为 18 , 则 $k$ 的值为
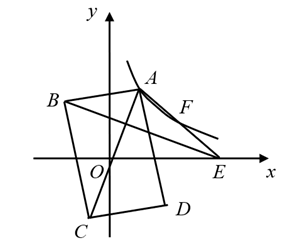
$\text{A.}$ 6
$\text{B.}$ 12
$\text{C.}$ 18
$\text{D.}$ 24
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若多边形的内角和是外角和的 2 倍, 则该多边形是 ( ) 边形.
现有四张正面分别标有数字 $-1,1,2,3$ 的不透明卡片, 它们除数字外其余完全相同, 将它们背而面朝 上洗均匀, 随机抽取一张, 记下数字后放回, 背面朝上洗均匀, 再随机抽取一张记下数字, 前后两次抽取 的数字分别记为 $m, n$, 则点 $P(m, n)$ 在第二象限的概率为
如图, 在边长为 2 的正方形 $A B C D$ 中, 对角线 $A C$ 的中点为 $O$, 分别以点 $A, C$ 为圆心, 以 $A O$ 的长为半 径画弧, 分别与正方形的边相交. 则图中的阴影部分的面积为 ( ) (结果保留 $\pi$ )
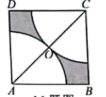
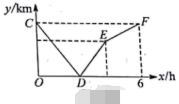
$\mathrm{A}, \mathrm{B}$ 两地相距 $240 \mathrm{~km}$, 甲货车从 A 地以 $40 \mathrm{~km} / \mathrm{h}$ 的速度匀速前往 $\mathrm{B}$ 地, 到达 $\mathrm{B}$ 地后停止, 在甲出发的同时, 乙货车从 $\mathrm{B}$ 地沿同一公路匀速前往 $\mathrm{A}$ 地, 到达 $\mathrm{A}$ 地后停止, 两车之间的路程 $y(\mathrm{~km})$ 与甲货车出发时间 $x$ (h)之间的函数关系如图中的折线 $C D-D E-E F$ 所示. 其中点 $\mathrm{C}$ 的坐标是 $(0,240)$, 点 $\mathrm{D}$ 的坐标是 $(2.4,0)$, 则点 $\mathrm{E}$ 的坐标是
火锅是重庆的一张名片, 深受广大市民的喜爱. 重庆某火锅店采取堂食、外卖、店外摆推 (简称摆摊) 三种 方式经营, 6月份该火锅店堂食、外卖、摆推三种方式的营业额之比为 3:5:2. 随着促进消费政策的出台, 该火锅店老板预计 7 月份总营业额会增加, 其中摆推增加的营业额占总增加的营业额的 $\frac{2}{5}$, 则摆推的营业 额将达到 7 月份总营业额的 $\frac{7}{20}$, 为使堂食、 外卖 7 月份的营业额之比为 8: 5 , 则 7 月份外卖还需增加的营 业额与 7 月份总营业额之比是
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算:
(1) $(x+y)^2+x(x-2 y)$;
(2) $\left(1-\frac{m}{m+3}\right) \div \frac{m^2-9}{m^2+6 m+9}$.
为了解学生掌握垃圾分类知识的情况, 增强学生环保意识, 某学校举行了 “垃圾分类人人有责” 的知识测试活 动, 现从该校七、八年级中各随机抽取 20 名学生的测试成绩 (满分 10 分, 6 分及 6 分以上为合格) 进行整 理、描述和分析, 下面给出了部分信息.
七年级 20 名学生的测试成绩为:
$$
7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,7,9,7,10,6 \text {. }
$$
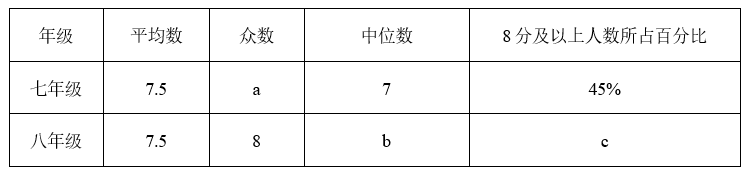
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、 8 分及以上人数所占百分比如下表所示:
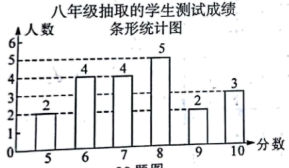
八年级20名学生的测试成绩条形统计图如图:
根据以上信息, 解答下列问题:
(1)直接写出上述表中的 $a, b, c$ 的值;
(2)根据以上数据, 你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好? 请说明理由(写出忈 条理由即可);
(3) 该校七、八年级共 1200 名学生参加了此次测试活动, 估计参加此次测试活动成绩合格的学生人数是 多少?
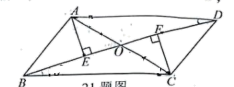
如图, 在平行四边形 $A B C D$ 中, 对角线 $A C, B D$ 相交于点 $O$, 分别过点 $A, C$ 作 $A E \perp B D, C F \perp B D$, 垂足分别为 $E, F . A C$ 平分 $\angle D A E$.
(1) 若 $\angle A O E=50^{\circ}$, 求 $\angle A C B$ 的度数;
(2) 求证: $A E=C F$.
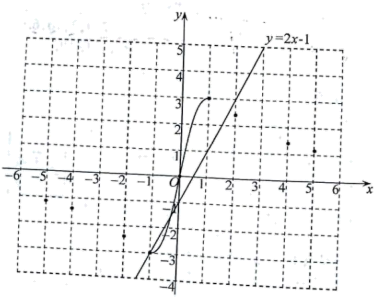
在初中阶段的函数学习中, 我们经历了列表、描点、连线画函数图象, 并结合图象研究函数性质的过程. 以 下是我们研究函数 $y=\frac{6 x}{x^2+1}$ 性质及其应用的部分过程, 请按要求完成下列各小题.
(1) 请把下表补充完整, 并在图中补全该函数图象;

(2)根据函数图象, 判断下列关于该函数性质的说法是否正确, 正确的在相应的括号内打“√“, 错误的在 相应的括号内打“ד;
①该函数图象是轴对称图形, 它的对称轴为 $y$ 轴; ( )
②该函数在自变量的取值范围内, 有最大值和最小值, 当 $x=1$ 时, 函数取得最大值 3 ; 当 $x=-1$ 时, 函数 取得最小值 $-3 ;(\quad)$
③当 $x < -1$ 或 $x>1$ 时, $y$ 随 $x$ 的增大而减小; 当 $-1 < x < 1$ 时, $y$ 随 $x$ 的增大而增大; ( )
(3) 已知函数 $y=2 x-1$ 的图象如图所示, 结合你所画的函数图象, 直接写出不等式 $\frac{6 x}{x^2+1}>2 x-1$ 的解集
(保留 1 位小数, 误差不超过 $0.2$ ).
在整数的除法运算中, 只有能整除与不能整除两种情况, 当不能整除时, 就会产生余数, 现在我们利用整 数的除法运算来研究一种数——“差一数”.
定义: 对于一个自然数, 如果这个数除以 5 余数为 4 , 且除以 3 余数为 2 , 则称这个数为“差一数”. 例如: $14 \div 5=2 \cdots \cdots 4,14 \div 3=4 \cdots \cdots 2$, 所以 14 是 “差一数”; $19 \div 5=3 \cdots \cdots 4$, 但 $19 \div 3=6 \cdots \cdots 1$, 所以 19 不是“差一数”.
(1) 判断 49 和 74 是否为“差一数”? 请说明理由;
(2) 求大于 300 且小于 400 的所有“差一数”.
为响应“把中国人的饭碗牢牢端在自己手中”的号召, 确保粮食安全, 优选品种, 提高产量, 某农业科技小组 对 $A 、 B$ 两个玉米品种进行实验种植对比研究. 去年 $A 、 B$ 两个品种各种植了 10 亩. 收获后 $A 、 B$ 两个品种 的售价均为 $2.4$ 元 $/ \mathrm{kg}$, 且 $B$ 品种的平均宙产量比 $A$ 品种高 100 千克, $A 、 B$ 两个品种全部售出后总收入为 21600 元
(1) 求 $A 、 B$ 两个品种去年平均亩产量分别是多少千克?
(2)今年, 科技小组优化了玉米的种植方法, 在保持去年种植面积不变的情况下, 预计 $A 、 B$ 两个品种平 均亩产量将在去年的基础上分别增加 $a \%$ 和 $2 a \%$. 由于 $B$ 品种深受市场欢迎, 预计每千克售价将在去年的基 础上上涨 $a \%$, 而 $A$ 品种的售价保持不变, $A 、 B$ 两个品种全部售出后总收人将增加 $\frac{20}{9} a \%$, 求 $a$ 的值.
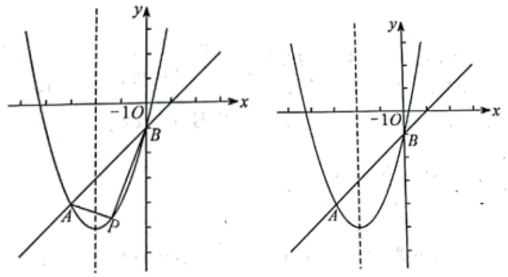
如图, 在平面直角坐标系中, 已知抛物线 $y=x^2+b x+c$ 与直线 $\mathrm{AB}$ 相交于 $\mathrm{A}, \mathrm{B}$ 两点, 其中 $A(-3,-4)$, $B(0,-1)$
(1)求该抛物线的函数表达式;
(2) 点 $\mathrm{P}$ 为直线 $\mathrm{AB}$ 下方抛物线上的任意一点, 连接 $\mathrm{PA}, \mathrm{PB}$, 求 $\triangle P A B$ 面积的最大值;
(3) 将该抛物线向右平移 2 个单位长度得到抛物线 $y=a_1 x^2+b_1 x+c_1\left(a_1 \neq 0\right)$, 平移后的抛物线与原抛物 线相交于点 $C$, 点 $D$ 为原抛物线对称轴上的一点, 在平面直角坐标系中是否存在点 $E$, 使以点 $B, C, D, E$ 为顶点的四边形为菱形, 若存在, 请直接写出点 $E$ 的坐标; 若不存在, 请说明理由.
如图, 在 $R t ~ \triangle A B C$ 中, $\angle B A C=90^{\circ}, A B=A C$, 点 $D$ 是 $B C$ 边上一动点, 连接 $A D$, 把 $A D$ 绕点 $A$ 逆时针旋 转 $90^{\circ}$, 得到 $A E$, 连接 $C E, D E$. 点 $F$ 是 $D E$ 的中点, 连接 $C F$.
(1) 求证: $C F=\frac{\sqrt{2}}{2} A D$;
(2) 如图 2 所示, 在点 $D$ 运动的过程中, 当 $B D=2 C D$ 时, 分别延长 $C F, B A$, 相交于点 $G$, 猜想 $A G$ 与 $B C$ 存在的数量关系, 并证明你猜想的结论;
(3) 在点 $D$ 运动的过程中, 在线段 $A D$ 上存在一点 $P$, 使 $P A+P B+P C$ 的值最小. 当 $P A+P B+P C$ 的值取 得最小值时, $A P$ 的长为 $m$, 请直接用含 $m$ 的式子表示 $C E$ 的长.