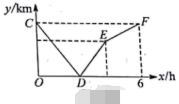
$\mathrm{A}, \mathrm{B}$ 两地相距 $240 \mathrm{~km}$, 甲货车从 A 地以 $40 \mathrm{~km} / \mathrm{h}$ 的速度匀速前往 $\mathrm{B}$ 地, 到达 $\mathrm{B}$ 地后停止, 在甲出发的同时, 乙货车从 $\mathrm{B}$ 地沿同一公路匀速前往 $\mathrm{A}$ 地, 到达 $\mathrm{A}$ 地后停止, 两车之间的路程 $y(\mathrm{~km})$ 与甲货车出发时间 $x$ (h)之间的函数关系如图中的折线 $C D-D E-E F$ 所示. 其中点 $\mathrm{C}$ 的坐标是 $(0,240)$, 点 $\mathrm{D}$ 的坐标是 $(2.4,0)$, 则点 $\mathrm{E}$ 的坐标是