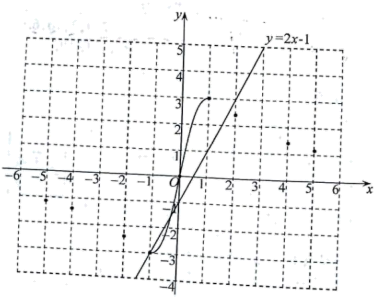
重庆市2020年初中学业水平暨高中招生考试-Kmath科数- 中考、高考、考验数学题库

在初中阶段的函数学习中, 我们经历了列表、描点、连线画函数图象, 并结合图象研究函数性质的过程. 以下是我们研究函数 $y=\frac{6 x}{x^2+1}$ 性质及其应用的部分过程, 请按要求完成下列各小题.
(1) 请把下表补充完整, 并在图中补全该函数图象;

（2）根据函数图象, 判断下列关于该函数性质的说法是否正确, 正确的在相应的括号内打“√“, 错误的在相应的括号内打“×“;
①该函数图象是轴对称图形, 它的对称轴为 $y$ 轴; ( )
②该函数在自变量的取值范围内, 有最大值和最小值, 当 $x=1$ 时, 函数取得最大值 3 ; 当 $x=-1$ 时, 函数取得最小值 $-3 ;(\quad)$
③当 $x < -1$ 或 $x > 1$ 时, $y$ 随 $x$ 的增大而减小; 当 $-1 < x < 1$ 时, $y$ 随 $x$ 的增大而增大; ( )
(3) 已知函数 $y=2 x-1$ 的图象如图所示, 结合你所画的函数图象, 直接写出不等式 $\frac{6 x}{x^2+1} > 2 x-1$ 的解集
(保留 1 位小数, 误差不超过 $0.2$ ).

0 人点赞

12 次查看

我来讲解

答案：

【详解】解: (1) 当 $\mathrm{x}=-3$ 时, $y=\frac{6 x}{x^2+1}=\frac{-18}{9+1}=-\frac{9}{5}$, 当 $\mathrm{x}=3$ 时, $y=\frac{6 x}{x^2+1}=\frac{18}{9+1}=\frac{9}{5}$, 函数图象如下:

(2)
①由函数图象可得它是中心对称图形, 不是轴对称图形;
故答案为: ×,
②结合函数图象可得: 该函数在自变量的取值范围内, 有最大值和最小值, 当 $x=1$ 时, 函数取得最大值 3 ; 当 $x=-1$ 时, 函数取得最小值 $-3$;
故答案为: √
③观察函数图象可得: 当 $x < -1$ 或 $x > 1$ 时, $y$ 随 $x$ 的增大而减小; 当 $-1 < x < 1$ 时, $y$ 随 $x$ 的增大而增大; 故答案为: √.

(3) $x < -1,-0.28 < x < 1.78(-0.28 \pm 0.2 < x < 1.78 \pm 0.2)$
$\frac{6 x}{x^2+1}=2 x-1$ 时, $(x+1)\left(2 x^2-3 x-1\right)=0$
得 $x_1=-1, x_2=\frac{3+\sqrt{17}}{4} \approx 1.8, \quad x_3=\frac{3-\sqrt{17}}{4} \approx-0.3$,
故该不等式的解集为: $\mathrm{x} < -1$ 或 $-0.3 < \mathrm{x} < 1.8$.

①点击首页查看更多试卷和试题 , 点击查看本题所在试卷
② 下载本题Word版或下载本题PDF版点击赞助本站

关闭