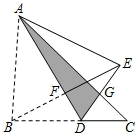
.如图, 三角形纸片 $A B C$, 点 $D$ 是 $B C$ 边上一点, 连接 $A D$, 把 $\triangle A B D$ 沿着 $A D$ 翻折, 得到 $V A E D, D E$ 与 $\mathrm{AC}$ 交于点 $G$, 连接 $B E$ 交 $A D$ 于点 $F$. 若 $D G=G E, A F=3, B F=2, \mathrm{~V} A D G$ 的面积为 2 , 则点 $F$ 到 $B C$ 的距离为
A
$\frac{\sqrt{5}}{5}$
B
$\frac{2 \sqrt{5}}{5}$
C
$\frac{4 \sqrt{5}}{5}$
D
$\frac{4 \sqrt{3}}{3}$
E
F