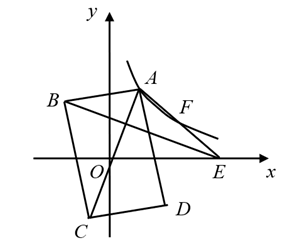
重庆市2020年初中学业水平暨高中招生考试-Kmath科数- 中考、高考、考验数学题库

如图, 在平面直角坐标系中, 矩形 $A B C D$ 的对角线 $A C$ 的中点与坐标原点重合, 点 $E$ 是 $x$ 轴上一点, 连接 $\mathrm{AE}$. 若 $\mathrm{AD}$ 平分 $\angle O A E$, 反比例函数 $y=\frac{k}{x}(k > 0, x > 0)$ 的图象经过 $\mathrm{AE}$ 上的两点 $\mathrm{A}, \mathrm{F}$, 且 $A F=E F, \triangle A B E$ 的面积为 18 , 则 $k$ 的值为

$ \text{A.}$ 6 $ \text{B.}$ 12 $ \text{C.}$ 18 $ \text{D.}$ 24

0 人点赞

20 次查看

我来讲解

答案：

解析：

解：

解: 如图, 连接 $\mathrm{BD}$,
$\because$ 四边形 $\mathrm{ABCD}$ 为矩形, $\mathrm{O}$ 为对角线,
$$
\therefore \mathrm{AO}=\mathrm{OD} \text {, }
$$
$$
\therefore \angle \mathrm{ODA}=\angle \mathrm{OAD} \text {, }
$$
又 $\because \mathrm{AD}$ 为 $\angle \mathrm{DAE}$ 的平分线,
$$
\begin{aligned}
& \therefore \angle \mathrm{OAD}=\angle \mathrm{EAD}, \\
& \therefore \angle \mathrm{EAD}=\angle \mathrm{ODA}, \\
& \therefore \mathrm{OB} / / \mathrm{AE} \\
& \because \mathrm{S}_{\triangle \mathrm{ABE}}=18 \\
& \therefore \mathrm{S}_{\triangle \mathrm{OAE}}=18
\end{aligned}
$$
设 $\mathrm{A}$ 的坐标为 $\left(\mathrm{a}, \frac{k}{a}\right)$,
$$
\because \mathrm{AF}=\mathrm{EF} \text {, }
$$
$\therefore \mathrm{F}$ 点的纵坐标为 $\frac{k}{2 a}$,
代入反比例函数解析式可得 $\mathrm{F}$ 点的坐标为 $\left(2 \mathrm{a}, \frac{k}{2 a}\right)$,
$\therefore \mathrm{E}$ 点的坐标为 $(3 \mathrm{a}, 0)$,
$\mathrm{S}_{\triangle \mathrm{OAE}}=\frac{1}{2} \times 3 \mathrm{a} \times \frac{k}{a}=18$,
解得 $\mathrm{k}=12$,
故选: B.

①点击首页查看更多试卷和试题 , 点击查看本题所在试卷
② 下载本题Word版或下载本题PDF版点击赞助本站

关闭