单选题 (共 10 题 ),每题只有一个选项正确
$-3$ 的倒数为
$\text{A.}$ $-\frac{1}{3}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $3$
$\text{D.}$ $-3$
函数 $y=\sqrt{1-x}$ 中自变量的取值范围是
$\text{A.}$ $x \geqslant 1$
$\text{B.}$ $x \leqslant 1$
$\text{C.}$ $x < 1$
$\text{D.}$ $x>1$
下列运算正确的是
$\text{A.}$ $5 a b-a b=4$
$\text{B.}$ $\frac{1}{a}+\frac{1}{b}=\frac{2}{a+b}$
$\text{C.}$ $a^6 \div a^2=a^4$
$\text{D.}$ $\left(a^2 b\right)^3=a^5 b^3$
一组数据 $12,8,10,7,13$ 的平均数和中位数分别是
$\text{A.}$ 9,10
$\text{B.}$ 9,8.5
$\text{C.}$ 10,8.5
$\text{D.}$ 10,10
如图, 一棵大树被台风拦腰刮断, 树根 $A$ 到刮断点 $P$ 的长度是 $4 m$, 折断部分 $P B$ 与地面成 $40^{\circ}$ 的夹角, 那 么原来树的长度是
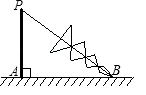
$\text{A.}$ $4+\frac{4}{\cos 40^{\circ}}$ 米
$\text{B.}$ $4+\frac{4}{\sin 40^{\circ}}$ 米
$\text{C.}$ $4+4 \sin 40^{\circ}$ 米
$\text{D.}$ $4+4 \cot 40^{\circ}$ 米
如图, 菱形 $A B C D$ 的对角线 $A C, B D$ 交于点 $O, A C=4, B D=16$, 将 $\triangle A B O$ 沿点 $A$ 到点 $C$ 的方向平移, 得 到 $\triangle A^{\prime} B^{\prime} O^{\prime}$. 当点 $A^{\prime}$ 与点 $C$ 重合时, 点 $A$ 与点 $B^{\prime}$ 之间的距离为

$\text{A.}$ 6
$\text{B.}$ 8
$\text{C.}$ 10
$\text{D.}$ 12
如图, 半径为 5 的 $\odot O$ 与正五边形 $A B C D E$ 相切于点 $B 、 E$, 则弧 $B E$ 的长为
$\text{A.}$ $4 \pi$
$\text{B.}$ $10 \pi$
$\text{C.}$ $15 \pi$
$\text{D.}$ $20 \pi$
已知 $m, n(m < n)$ 是关于 $x$ 的方程 $(x-a)(x-b)=-3$ 的两根, 若 $a < b$, 则下列判断正确的是
$\text{A.}$ $a < m < b < n$
$\text{B.}$ $m < a < n < b$
$\text{C.}$ $a < m < n < b$
$\text{D.}$ $m < a < b < n$
在矩形 $A B C D$ 中, 点 $E$ 为 $A D$ 中点, 点 $F$ 为 $C D$ 中点, 连接 $B F 、 C E$ 交于点 $G$, 若 $A B=4, \angle D C E=2 \angle C B F$, 则线段 $B G$ 的长为
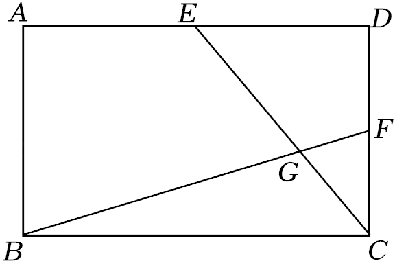
$\text{A.}$ $\frac{8 \sqrt{10}}{5}$
$\text{B.}$ $2 \sqrt{10}$
$\text{C.}$ $4$
$\text{D.}$ $\frac{3}{2} \sqrt{10}$
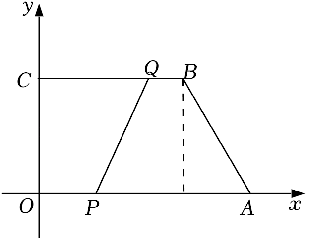
已知线段 $A B, \odot M$ 经过 $A 、 B$ 两点, 若 $90^{\circ} \leqslant \angle A M B \leqslant 120^{\circ}$, 则称点 $M$ 是线段 $A B$ 的 “好心”; $\odot M$ 上的 点称作线段 $A B$ 的 “闪光点”. 已知 $A(2,0), B(6,0)$.
(1)点 $M(4,2)$ 是线段 $A B$ 的 “好心”;
(2)若反比例函数 $y=\frac{\mathrm{k}}{\mathrm{x}}$ 上存在线段 $A B$ 的 “好心”, 则 $\frac{8 \sqrt{3}}{3} \leqslant k \leqslant 8$;
(3)线段 $A B$ 的 “闪光点” 组成的图形既是轴对称图形, 又是中心对称图形;
(4)若直线 $y=x+b$ 上存在线段 $A B$ 的 “闪光点”, 则 $-10 \leqslant b \leqslant 2$.
下来说法正确的是
$\text{A.}$ (1)(2)(3)(4)
$\text{B.}$ (1)(3)(4)
$\text{C.}$ (1)(3)
$\text{D.}$ (1)(2)
填空题 (共 8 题 ),请把答案直接填写在答题纸上
2022 年江苏省约有 359000 名考生报名参加普通高考, 数据 “ 359000 ” 用科学记数法可表示为
反比例函数 $y=\frac{\mathrm{k}}{\mathrm{x}}$ 与一次函数 $y=x+2$ 的图象交于点 $A(-1, a)$, 则 $k=$
关于 $x$ 的方程 $x^2-3 x+k=0$.
(1) 若该方程有一个根为 $x=1$, 则 $k=$
(2) 若该方程有两个实数根, 则 $k$ 的取值范围是
请举反例说明命题 “对于任意实数 $x, x^2+5 x+5$ 的值总是正数” 是假命题, 你举的反例是 $x=$ (写出一个 $x$ 的值即可).
如图, 在 $\triangle A B C$ 中, $A B=6$, 以点 $A$ 为圆心, 3 为半径的圆与边 $B C$ 相切于点 $D$, 与 $A C, A B$ 分别交于点 $E$ 和点 $G$, 点 $F$ 是 $\odot O$ 上一点 (不与 $G 、 E$ 重合), $\angle C D E=18^{\circ}$, 则 $\angle G F E$ 的度数是
如图, 在边长为 1 的正方形 $A B C D$ 中放入四个小正方形后形成一个中心对称图形, 其中两顶点 $E 、 F$ 公别在 边 $B C 、 A D$ 上, 则放入的四个小正方形的面积之和为
如图, 在平面直角坐标系中, 四边形 $O A B C$ 的顶点坐标分别为 $O(0,0), A(12,0), B(8,6), C(0,6)$. 动 点 $P$ 从点 $O$ 出发, 以每秒 3 个单位长度的速度沿边 $O A$ 向终点 $A$ 运动; 动点 $Q$ 从点 $B$ 同时出发, 以每秒 2 个 单位长度的速度沿边 $B C$ 向终点 $C$ 运动. 设运动的时间为 $t$ 秒, 则 $\frac{\mathrm{BQ}}{\mathrm{OP}}=$ ; 作 $A G \perp P Q$ 于点 $G, A G$ 的 最大值是
解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1) 计算: $-\left|-\frac{1}{2}\right|+(-2)^{-1}-3 \tan 45^{\circ}$;
(2) 化简: $(a+b)^2-(2 a+b)(2 a-b)$.
(1) 解方程: $2 x^2+4 x-1=0$;
(2) 解不等式组 $\left\{\begin{array}{l}5 x-2>3(x+1) \\ \frac{1}{2} x-1 \leqslant 7-\frac{3}{2} x\end{array}\right.$.
如图, 在 $\square A B C D$ 中, 过点 $D$ 作 $D E \perp A B$ 于点 $E$, 点 $F$ 在边 $C D$ 上, $D F=B E$, 连接 $A F, B F$.
(1) 求证: 四边形 $B F D E$ 是矩形;
(2) 若 $C F=3, B F=4, D F=5$, 求证: $A F$ 平分 $\angle D A B$.
为弘扬中华传统文化, 黔南州近期举办了中小学生 “国学经典大赛”. 比赛项目为: $A$. 唐诗; $B$. 宋 词; C. 论语; D. 三字经. 比赛形式分 “单人组” 和 “双人组”.
(1)小丽参加 “单人组”, 她从中随机抽取一个比赛项目,恰好抽中 “三字经” 的概率是多少?
(2)小红和小明组成一个小组参加 “双人组” 比赛, 比赛规则是: 同一小组的两名队员的比赛项目不能相同, 且每人只能随机抽取一次, 则恰好小红抽中 “唐诗” 且小明抽中 “宋词” 的概率是多少? 请用画树状图或列 表的方法进行说明.
某区组织学生参加党史知识竞赛, 从中抽取了 200 名学生的成绩 (得分取正整数, 满分为 100 分) 进行统计, 根据成绩分成如下 5 组:
$$
\begin{aligned}
& \text { A.50.5 } \sim 0.5 \\
& \text { B.60.5 } 70.5 \\
& \text { C.70.5 } \sim 80.5 \\
& \text { D.80.5 } 90.5 \\
& \text { E.90.5 } 100.5
\end{aligned}
$$
并绘制成两个统计图.

(1) $a=$, $b=$, $n=$
(2) 求 $E$ 组共有多少人?
(3) 该区共有 1200 名学生参加党史知识竞赛, 如果设定一等奖的分数不低于 91 分, 那么请你估计全区获得一等奖的人数是多少?
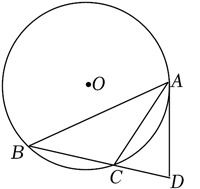
如图, $\odot O$ 是 $\triangle A B C$ 的外接圆, 点 $D$ 在 $B C$ 延长线上, 且满足 $\angle C A D=\angle B$.
(1) 求证: $A D$ 是 $\odot O$ 的切线;
(2) 若 $A C$ 是 $\angle B A D$ 的平分线, $\sin B=\frac{3}{5}, B C=4$, 求 $\odot O$ 的半径.
如图, 在 $\triangle A B C$ 中, $A B=B C, \angle A B C=90^{\circ}$, 动点 $E$ 在 $\angle A B C$ 外部, 且 $\angle A B C=2 \angle A E C$.
(1) 利用尺规作图在图 1 中作出一个符合题意的点 $E$; (不写作法, 保留作图痕迹)
(2) 如图 2, 若 $F$ 是 $A C$ 的中点, 线段 $B E$ 与线段 $E F$ 的长度存在怎样的等量关系? 请说明理由.
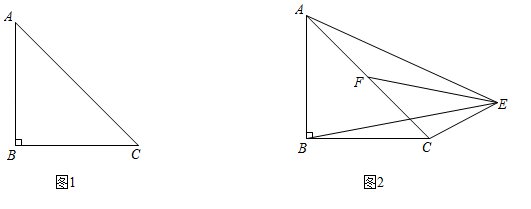
商店销售一种商品, 经市场调查发现: 在实际销售中, 售价 $x$ 为整数, 且该商品的月销售量 $y$ (件) 是售价 $x$ (元/件) 的一次函数, 其售价 $x$ (元/件)、月销售量 $y$ (件)、月销售利润 $w$ (元) 的部分对应值如表:

注: 月销售利润 $=$ 月销售量 $\times($ 售价 $-$ 进价 $)$
(1) 求 $y$ 关于 $x$ 的函数表达式;
(2)当该商品的售价是多少元时, 月销售利润最大? 并求出最大利润;
(3)现公司决定每销售 1 件商品就捐赠 $m$ 元利润 ( $m \leqslant 6$ ) 给 “精准扶贫” 对象, 要求: 在售价不超过 52 元时, 每天扣除捐赠后的日销售利润随售价 $x$ 的增大而增大, 求 $m$ 的取值范围.
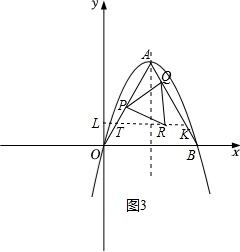
在平面直角坐标系 $x O y$ 中, 抛物线 $y=a x^2-4 a x+c$ 与 $x$ 轴交于原点 $O$, 点 $B$, 顶点 $A$ 在第一象限, 且满足 $O A=O B$.
(1) 求二次函数表达式;
(2) 过点 $O$ 作 $A B$ 的平行线 $O T$, 在边 $A B$ 右侧的抛物线上有一点 $C$, 过点 $C$ 作 $y$ 轴的平行线, 交 $A B$ 于点 $D$, 交 $x$ 轴于点 $E$, 交 $O T$ 于 $F$, 过点 $C$ 作 $C G \perp A B$ 于点 $G$, 当 $\frac{S_{\triangle C G D}}{S_{\triangle O E F}}=\frac{1}{48}$ 时, 求点 $C$ 的坐标;
(3) 点 $P$ 是线段 $O A$ 的中点, 点 $Q$ 是线段 $A B$ 上一动点, 连接 $P Q$, 将线段 $P Q$ 绕点 $P$ 顺时针旋转 $60^{\circ}$ 得到 $P R$, 设 $R(m, n)$, 请直接写出 $m$ 与 $n$ 满足的函数关系式.
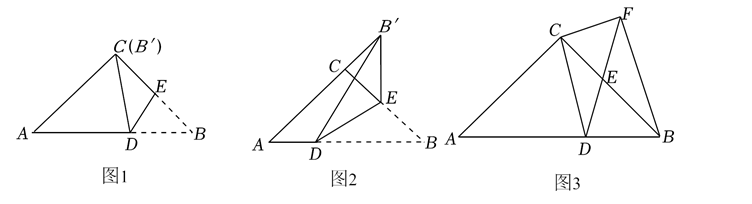
在 $\triangle A B C$ 中, $A C=B C=5, \tan B=\frac{3}{4}$, 点 $D 、$ 点 $E$ 分别是 $A B 、 B C$ 边上的动点.
(1) 连接 $D E$, 作 $\triangle B D E$ 关于 $D E$ 的对称图形 $\triangle B^{\prime} D E$.
(1) 如图 1, 当点 $B^{\prime}$ 恰好与点 $C$ 重合, 求 $D E$ 的长;
(2)如图 2, 当点 $B^{\prime}$ 落在 $A C$ 的延长线上, 且 $B^{\prime} E \perp A B$, 求 $B D$ 的长;
(2) 在点 $D 、 E$ 运动过程中, 满足 $C D^2=C E \cdot C B$, 过点 $C$ 作 $C F \perp C D$ 交射线 $D E$ 于点 $F$, 是否存在某个位置,
使得 $F D=F B$ ? 若存在, 求出此时 $A D$ 的长; 若不存在, 请说明理由.