在平面直角坐标系 $x O y$ 中, 抛物线 $y=a x^2-4 a x+c$ 与 $x$ 轴交于原点 $O$, 点 $B$, 顶点 $A$ 在第一象限, 且满足 $O A=O B$.
(1) 求二次函数表达式;
(2) 过点 $O$ 作 $A B$ 的平行线 $O T$, 在边 $A B$ 右侧的抛物线上有一点 $C$, 过点 $C$ 作 $y$ 轴的平行线, 交 $A B$ 于点 $D$, 交 $x$ 轴于点 $E$, 交 $O T$ 于 $F$, 过点 $C$ 作 $C G \perp A B$ 于点 $G$, 当 $\frac{S_{\triangle C G D}}{S_{\triangle O E F}}=\frac{1}{48}$ 时, 求点 $C$ 的坐标;
(3) 点 $P$ 是线段 $O A$ 的中点, 点 $Q$ 是线段 $A B$ 上一动点, 连接 $P Q$, 将线段 $P Q$ 绕点 $P$ 顺时针旋转 $60^{\circ}$ 得到 $P R$, 设 $R(m, n)$, 请直接写出 $m$ 与 $n$ 满足的函数关系式.
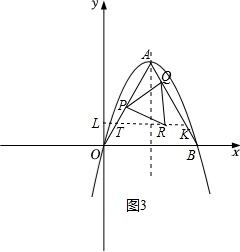
(1) 求二次函数表达式;
(2) 过点 $O$ 作 $A B$ 的平行线 $O T$, 在边 $A B$ 右侧的抛物线上有一点 $C$, 过点 $C$ 作 $y$ 轴的平行线, 交 $A B$ 于点 $D$, 交 $x$ 轴于点 $E$, 交 $O T$ 于 $F$, 过点 $C$ 作 $C G \perp A B$ 于点 $G$, 当 $\frac{S_{\triangle C G D}}{S_{\triangle O E F}}=\frac{1}{48}$ 时, 求点 $C$ 的坐标;
(3) 点 $P$ 是线段 $O A$ 的中点, 点 $Q$ 是线段 $A B$ 上一动点, 连接 $P Q$, 将线段 $P Q$ 绕点 $P$ 顺时针旋转 $60^{\circ}$ 得到 $P R$, 设 $R(m, n)$, 请直接写出 $m$ 与 $n$ 满足的函数关系式.
