单选题 (共 13 题 ),每题只有一个选项正确
集合 $A=\{0,1,2\}$, 集合 $B=\{-2,0,1\}$, 则 $A \cap B=$
$\text{A.}$ $\{0,1\}$
$\text{B.}$ $\{-2,0\}$
$\text{C.}$ $\{-2,1,0\}$
$\text{D.}$ $\{0,1,2\}$
若复数 $z$ 满足 $(3-4 i) z=1$, 则 $|z|=$
$\text{A.}$ $1$
$\text{B.}$ $\frac{1}{5}$
$\text{C.}$ $\frac{1}{7}$
$\text{D.}$ $\frac{1}{25}$
已知非零向量 $\vec{a}, \vec{b}$ 满足 $|\vec{b}|=2|\vec{a}|$, 且 $\vec{a} \perp(\vec{a}-b)$, 则 $\vec{a}$ 与 $\vec{b}$ 的夹角为
$\text{A.}$ $\frac{\pi}{3}$
$\text{B.}$ $\frac{\pi}{2}$
$\text{C.}$ $\frac{2 \pi}{3}$
$\text{D.}$ $\frac{5 \pi}{6}$
已知 $\tan \left(\theta+\frac{\pi}{4}\right)=\frac{1}{2} \tan \theta-\frac{7}{2}$, 则 $\cos 2 \theta=$
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $-\frac{4}{5}$
$\text{D.}$ $\frac{4}{5}$
已知函数 $f(x)=\sin 2 x$ 和直线 $l: y=2 x+a$, 那么 “直线 $l$ 与曲线 $y=f(x)$ 相切” 是 “ $a=0$ ”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充分必要条件
$\text{D.}$ 既不充分也不必要条件
已知 $a, b$ 为非负实数, 且 $a+2 b=1$, 则 $\frac{a^2+1}{a}+\frac{2 b^2+1}{b}$ 的最小值为
$\text{A.}$ $1+2 \sqrt{2}$
$\text{B.}$ $2+2 \sqrt{2}$
$\text{C.}$ $3+2 \sqrt{2}$
$\text{D.}$ $4+2 \sqrt{2}$
已知三棱锥 $S-A B C$ 如图所示, $A S, A B, A C$ 两两垂直, 且 $|A S|=|A B|=|A C|=2 \sqrt{2}$, 点 $E, F$ 分别是棱 $A S, B S$ 的中点, 点 $G$ 是棱 $S C$靠近点 $C$ 的四等分点, 则空间几何体 $E F G-A B C$ 的体积为
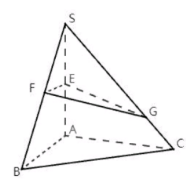
$\text{A.}$ $\frac{11 \sqrt{2}}{6}$
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ $\frac{13 \sqrt{2}}{6}$
$\text{D.}$ $\frac{7 \sqrt[3]{2}}{3}$
已知数列 $\left\{a_k\right\}$ 为有穷整数数列,具有性质 $p$ : 若对任意的 $n \in\{1,2,3,4\}$ , $\left\{a_k\right\}$ 中存在 $a_i, a_{i+1}, a_{i+2}, \cdots, a_{i+j}\left(i \geq 1, j \geq 0, i, j \in N^*\right)$, 使得 $a_i+a_{i+1}+a_{i+2}+\cdots+a_{i+j}=n$, 则称 $\left\{a_k\right\}$ 为 $4-$ 连续可表数列. 下面数列为 $4-$ 连续可表数列的是
$\text{A.}$ $1,1,1$
$\text{B.}$ $1,1,2$
$\text{C.}$ $1,3,1$
$\text{D.}$ $2,3,6$
关于平面向量, 有下列四个命题, 其中说法正确的是
$\text{A.}$ $\vec{a}=\left(\frac{9}{2}, k\right), \vec{b}=(k, 8)$, 若 $\vec{a} / / \vec{b}$, 则 $k=6$
$\text{B.}$ 若 $\vec{a} \cdot \vec{c}=\vec{b} \cdot \vec{c}$ 且 $\bar{c} \neq \overrightarrow{0}$, 则 $\vec{a}=\vec{b}$
$\text{C.}$ 若点 $G$ 是 $\triangle A B C$ 的雨心, 则 $\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}=\overrightarrow{0}$
$\text{D.}$ 若向量 $\vec{a}=(-1,1), \vec{b}=(2,3)$, 则向量 $\vec{b}$ 在向屋 $\vec{a}$ 上的投影向量为 $\frac{\vec{a}}{2}$
已知函数 $f(x)=\cos ^2 x+\sin x \cos x-\frac{1}{2}$ 的图象为 $C$, 以下说法中正确的是
$\text{A.}$ 函数 $f(x)$ 的最大值为 $\frac{\sqrt{2}+1}{2}$
$\text{B.}$ 图象 $C$ 相邻两条对称轴的距离为 $\frac{\pi}{2}$
$\text{C.}$ 图象 $C$ 关于 $\left(-\frac{\pi}{8}, 0\right)$ 中心对称
$\text{D.}$ 要得到函数 $y=\frac{\sqrt{2}}{2} \sin x$ 的图象, 只需将函数 $f(x)$ 的图象横坐标伸长为原来的 2 倍, 再向右平移 $\frac{\pi}{4}$ 个单位
若函数 $f(x)$ 的定义域为 $D$, 若对于任意 $x_1 \in D$, 都存在唯一的 $x_2 \in D$, 使得 $f\left(x_1\right)+f\left(x_2\right)=1$,则称 $f(x)$ 为 “ $I$ 型函数”, 则下列说法正确的是
$\text{A.}$ 函数 $f(x)=\ln x$ 是 “ $I$ 型函数”
$\text{B.}$ 函数 $f(x)=\sin x$ 是 “ $I$ 型函数”
$\text{C.}$ 若函数 $f(x)$ 是 “ $I$ 型函数”, 则函数 $1-f(x)$ 也是 “ $I$ 型函数”
$\text{D.}$ 已知 $m \in R$, 若 $f(x)=m+\sin x, x \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ 是 “ $I$ 型函数”, 则 $m=\frac{1}{2}$
已知棱长为 1 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $P$ 为线段 $A_1 C$ 上一动点, 则下列判断正确的是
$\text{A.}$ 存在点 $P$, 使得 $C_1 P / / A B_1$
$\text{B.}$ 三棱椎 $P-B C_1 D$ 的外接球半径最小值为 $\frac{\sqrt{6}}{3}$
$\text{C.}$ 当 $P$ 为 $A_1 C$ 的中点时, 过 $P$ 与平面 $B C_1 D$ 平行的平面截正方体所得的截面面积为 $\frac{3 \sqrt{3}}{4}$
$\text{D.}$ 存在点 $P$, 使得点 $P$ 到直线 $B_1 C_1$ 的距离为 $\frac{4}{5}$
已知棱长为 1 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $P$ 为线段 $A_1 C$ 上一动点, 则下列判断正确的是
$\text{A.}$ 存在点 $P$, 使得 $C_1 P / / A B_1$
$\text{B.}$ 三棱椎 $P-B C_1 D$ 的外接球半径最小值为 $\frac{\sqrt{6}}{3}$
$\text{C.}$ 当 $P$ 为 $A_1 C$ 的中点时, 过 $P$ 与平面 $B C_1 D$ 平行的平面截正方体所得的截面面积为 $\frac{3 \sqrt{3}}{4}$
$\text{D.}$ 存在点 $P$, 使得点 $P$ 到直线 $B_1 C_1$ 的距离为 $\frac{4}{5}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
关于 $x$ 的不等式 $a x^2+(a+b) x+2>0$ 的解集为 $(-3,1)$, 则 $a+b=$
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和 $S_n=2^n-1$, 则 $\log _2 a_{10}=$
已知函数 $f(x)=\left\{\begin{array}{l}\left|2^x-1\right|, x \leq 1 \\ (x-2)^2, x>1\end{array}\right.$, 关于 $x$ 的方程 $f^2(x)-a \cdot f(x)=0$ 有六个不等的实根, 则实数 $a$ 的取值范围是
如图, 已知函数 $f(x)=A \sin (\omega x+\varphi)$ (其中 $A>0, \omega>0,|\varphi| \leq \frac{\pi}{2}$ )的图象与 $x$ 轴交于点 $A, B$, 与 $y$ 轴交于点 $C, \overrightarrow{B C}=2 \overrightarrow{B D}, \angle O C B=\frac{\pi}{3}$, $|O A|=2,|A D|=\frac{2 \sqrt{21}}{3}$, 则函数 $f(x)$ 在 $[1,6]$ 上的值域为

解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $S_n$ 为数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 且 $a_1=1, n S_{n+1}=(n+1) S_n+n^2+n, n \in N^*$
(1) 证明: 数列 $\left\{\frac{S_n}{n}\right\}$ 为等差数列, 并求 $\left\{S_n\right\}$ 的通项公式;
(2) 若 $b_n=\frac{1}{a_n \cdot a_{n+1}}$, 设数列 $\left\{b_n\right\}$ 的前 $n$ 项和为 $T_n$, 求 $T_n$.
在 $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c$, 且 $b \cos A+a \cos B=-2 c \cos A$.
(1) 求角 $A$ 的值;
(2) 已知点 $D$ 为 $B C$ 的中点, 且 $A D=2$, 求 $a$ 的最大值.
若二次函数 $f(x)$ 满足 $f(x+1)+f(x)=-x^2-5 x-\frac{5}{2}$
(1) 求 $f(x)$ 的解析式;
(2) 若函数 $g(x)=x \ln x+f(x)$, 解关于 $x$ 的不等式: $g\left(x^2+x\right) \geq g(2)$.
如图 (1) 所示, 在 $\triangle A B C$ 中, $\angle A B C=60^{\circ}$, 过点 $A$ 作 $A D \perp B C$, 坓足 $D$ 在线段 $B C$ 上,且 $A D=2 \sqrt{3}, C D=\sqrt{5}$, 沿 $A D$ 将 $\triangle C D A$ 折起 (如图 (2)), 点 $E, F$ 分别为棱 $A C, A B$ 的中点.
(1) 证明: $A D \perp E F$;
(2) 若二面角 $C-D A-B$ 所成角的正切值为 2 , 求二面角 $C-D F-E$ 所成角的余弦值.
已知数列 $\left\{a_n\right\}$ 是公比大于 0 的等比数列, $a_1=4, a_3=64$. 数列 $\left\{b_n\right\}$ 满足: $b_n=a_{2 n}+\frac{1}{a_n}$ $\left(n \in N^*\right)$.
(1) 求数列 $\left\{b_n\right\}$ 的通项公式:
(2) 证明: $\left\{b_n^2-b_{2 n}\right\}$ 是等比数列;
(3) 证明: $\sum_{k=1}^n \sqrt{\frac{(2 k-1)(2 k+1)}{b_k^2-b_{2 k}}} < 2 \sqrt{2}$.
已知函数 $f(x)=x(t-\ln x), t \in R$
(1) 讨论函数 $f(x)$ 的单调区间;
(2) 当 $t=1$ 时, 设 $x_1, x_2$ 为两个不相等的正数, 且 $f\left(x_1\right)=f\left(x_2\right)=a$, 证明: $x_1+x_2>a(2-e)+e-\frac{1}{e}$.