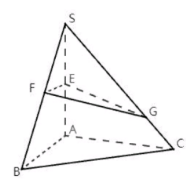
已知三棱锥 $S-A B C$ 如图所示, $A S, A B, A C$ 两两垂直, 且 $|A S|=|A B|=|A C|=2 \sqrt{2}$, 点 $E, F$ 分别是棱 $A S, B S$ 的中点, 点 $G$ 是棱 $S C$靠近点 $C$ 的四等分点, 则空间几何体 $E F G-A B C$ 的体积为

A. $\frac{11 \sqrt{2}}{6}$
B. $2 \sqrt{2}$
C. $\frac{13 \sqrt{2}}{6}$
D. $\frac{7 \sqrt[3]{2}}{3}$