单选题 (共 8 题 ),每题只有一个选项正确
设全集 $U=\{-2,-1,0,1,2\}$, 集合 $A=\left\{x \in \mathbf{N} \mid y=\lg (2-x)+\frac{1}{\sqrt{x+2}}\right\}$, 则 $\complement_U A=$
$\text{A.}$ $\{-2,-1,2\}$
$\text{B.}$ $\{-2,2\}$
$\text{C.}$ $\varnothing$
$\text{D.}$ $\{-2,-1,0,2\}$
已知复数 $z=1-\mathrm{i}^{23}$, 且 $\bar{z}=a+b z^2$, 其中 $a, b$ 为实数, 则 $a-b=$
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{3}{2}$
$\text{D.}$ $2$
已知向量 $\boldsymbol{a}, \boldsymbol{b}$ 满足 $|\boldsymbol{a}|=3|\boldsymbol{b}|=|\boldsymbol{a}-2 \boldsymbol{b}|=3$, 则 $\boldsymbol{a} \cdot(\boldsymbol{a}-\boldsymbol{b})=$
$\text{A.}$ 8
$\text{B.}$ 9
$\text{C.}$ 14
$\text{D.}$ 23
角谷猜想” 首先流传于美国, 不久便传到欧洲, 后来一位名叫角谷静夫的日本人又把它带到 亚洲, 因而人们就顺势把它叫作“角谷猜想”. “角谷猜想”是指一个正整数, 如果是奇数就乘以 3 再加 1 , 如果是偶数就除以 2 , 这样经过若干次运算, 最终回到 1 . 对任意正整数 $a_0$, 记按照上 述规则实施第 $n$ 次运算的结果为 $a_n(n \in \mathbf{N})$, 若 $a_5=1$, 且 $a_i(i=1,2,3,4)$ 均不为 1 , 则 $a_0=$
$\text{A.}$ 5 或 16
$\text{B.}$ 5 或 32
$\text{C.}$ 3 或 8
$\text{D.}$ 7 或 32
已知函数 $f(x)$ 的部分图象如图所示, 则 $f(x)$ 的解析式可能为

$\text{A.}$ $f(x)=x \cos \pi(x+1)$
$\text{B.}$ $f(x)=(x-1) \cos \pi x$
$\text{C.}$ $f(x)=(x-1) \sin \pi x$
$\text{D.}$ $f(x)=x^3-2 x^2+x-1$
已知正四棱雉 (底面为正方形, 且顶点在底面的射影为正方形的中心的棱雉为正四棱雉) $P-A B C D$ 的底面正方形边长为 2 , 其内切球 $O$ 的表面积为 $\frac{\pi}{3}$, 动点 $Q$ 在正方形 $A B C D$ 内运 动, 且满足 $O Q=O P$, 则动点 $Q$ 形成轨迹的周长为
$\text{A.}$ $\frac{2 \pi}{11}$
$\text{B.}$ $\frac{3 \pi}{11}$
$\text{C.}$ $\frac{4 \pi}{11}$
$\text{D.}$ $\frac{5 \pi}{11}$
2022 年 7 月 24 日 14 时 22 分, 搭载我国首个科学实验舱问天实验舱的长征五号$\mathrm{B}$ 遥三 运载火箭成功发射, 令世界瞩目. 为弘扬航天精神, $\mathrm{M}$ 大学举办了 “逐梦星辰大海一一航天 杯”知识竞赛, 竞赛分为初赛和复赛, 初赛通过后进人复赛, 复赛通过后颁发相应荣誉证书和奖品. 为鼓励学生积极参加, 学校后勤部给予一定的奖励: 只参加了初赛的学生奖励 50 元的奖品, 参加 了复赛的学生再奖励 100 元的奖品. 现有 $A, B, C$ 三名学生报名参加了这次竞赛, 已知 $A$ 通 过初赛、复赛的概率分别为 $\frac{1}{2}, \frac{1}{3} ; B$ 通过初赛、复赛的概率分别为 $\frac{2}{3}, \frac{1}{2}, C$ 通过初赛和复赛 的概率与 $B$ 完全相同. 记这三人获得后勤部的奖品总额为 $X$ 元, 则 $X$ 的数学期望为
$\text{A.}$ 300 元
$\text{B.}$ $\frac{1000}{3}$ 元
$\text{C.}$ 350 元
$\text{D.}$ $\frac{2000}{3}$ 元
过椭圆 $C: \frac{x^2}{4}+\frac{y^2}{3}=1$ 上的点 $A\left(x_1, y_1\right), B\left(x_2, y_2\right)$ 分别作 $C$ 的切线, 若两切线的交点恰好在 直线 $l: x=4$ 上, 则 $y_1 \cdot y_2$ 的最小值为
$\text{A.}$ $-\frac{3}{2}$
$\text{B.}$ $-\frac{9}{4}$
$\text{C.}$ $-9$
$\text{D.}$ $\frac{9}{4}$
多选题 (共 4 题 ),每题有多个选项正确
在新冠疫情防控常态化的背景下, 为提高疫情防控意识, 某学校举办了一次疫情防控知识竞 赛 (满分 100 分), 并规定成绩不低于 90 分为优秀. 现该校从高一、高二两个年级分别随机抽 取了 10 名参赛学生的成绩(单位: 分), 如下表所示:

则下列说法正确的是
$\text{A.}$ 高一年级所抽取参赛学生成绩的中位数为 91 分
$\text{B.}$ 高二年级所抽取参赛学生成绩的众数为 94 分
$\text{C.}$ 两个年级所抽取参赛学生的优秀率相同
$\text{D.}$ 两个年级所抽取参赛学生的平均成绩相同
已知抛物线 $C: y^2=2 p x(p>0)$ 的焦点为 $F(4,0)$, 点 $A, B$ 在 $C$ 上, 且弦 $A B$ 的中点到直线 $x=-2$ 的距离为 5 , 则
$\text{A.}$ $p=16$
$\text{B.}$ 线段 $A B$ 的长为定值
$\text{C.}$ $A, B$ 两点到 $C$ 的准线的距离之和为 14
$\text{D.}$ $|A F| \cdot|B F|$ 的最大值为 49
如图, 在直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 中, 底面 $A B C D$ 为菱形, 且 $D E \perp A_1 C$, 垂足为 $E$, 则
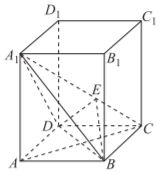
$\text{A.}$ $A A_1 \perp B D$
$\text{B.}$ $A A_1 / /$ 平面 $B D E$
$\text{C.}$ 平面 $B D E \perp$ 平面 $A_1 C D$
$\text{D.}$ $B E \perp$ 平面 $A_1 C D$
已知函数 $f(x+4)$ 是定义在 $\mathbf{R}$ 上的奇函数, 函数 $g(x+2)$ 是定义在 $\mathbf{R}$ 上的偶函数, 且满足 $g(x)=(x-2) f(x-1), g(3)=g(4)+2=6$, 则
$\text{A.}$ $f(x)$ 的图象关于点 $(1,0)$ 对称
$\text{B.}$ $f(x)$ 是周期为 3 的周期函数
$\text{C.}$ $f(1)=0$
$\text{D.}$ $\sum_{i=1}^{2026} f(i)=8$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
中国共产党第二十次全国代表大会在北京召开期间, 将含甲、乙在内的 8 名工作人员平均分配到 $A, B$ 两个省代表厅从事服务工作,则甲、乙两人不分在同一省代表厅的概率为
已知圆 $x^2+y^2=a$ 与圆 $x^2+y^2+4 x+2 y+b=0$ 交于 $M, N$ 两点, 若 $|M N|=\frac{8 \sqrt{5}}{5}$, 则实数 $a$, $b$ 的一对值可以为 $a=$ ,$b=$ . (写出满足条件的一组即可)
已知函数 $ f(x)=\left|\sin \frac{\omega x}{2}\right|+\left|\cos \frac{\omega x}{2}\right|(\omega>0) $ 在区间 $ \left(\frac{\pi}{3}, \frac{3 \pi}{4}\right) $ 上单调递增, 则 $ \omega $ 的取值范围
若函数 $f(x)=a x^3-3 \mathrm{e}^x+2023(a \in \mathbf{R})$ 有且仅有一个极值点, 则 $a$ 的取值范围是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
记 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 已知 $2 \sin A \sin C \cos B+\cos B=3 \sin ^2 B-$ $\cos (A-C)$.
(1) 证明: $a+c=2 b$;
(2) 若 $b=2, \cos B=\frac{5}{13}$, 求 $\triangle A B C$ 的面积.
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $\frac{1}{8} S_n=2^{n-2}-\frac{1}{4}$.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 记 $b_n=\frac{a_{n+1}}{\left(a_n-1\right) \cdot\left(a_{n+1}-1\right)}$, 数列 $\left\{b_n\right\}$ 的前 $n$ 项和为 $T_n$, 若不等式 $2\left(2^{n+1}-1\right) T_n < \lambda+$ $a_n^2$ 对任意 $n \in \mathbf{N}^*$ 恒成立, 求实数 $\lambda$ 的取值范围.
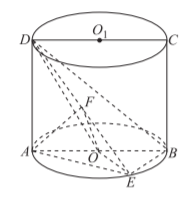
如图, 矩形 $A B C D$ 是圆柱 $O O_1$ 的一个轴截面, 点 $E$ 在圆 $O$ 上, $A D=A E=3$, 且 $\angle A B E=$ $60^{\circ}, \overrightarrow{E F}=\lambda \overrightarrow{E D}(0 \leqslant \lambda \leqslant 1)$.
(1) 当 $\lambda=\frac{1}{2}$ 时,证明: 平面 $O A F \perp$ 平面 $B D E$;
(2) 若直线 $A F$ 与平面 $O D E$ 所成角的正弦值为 $\frac{\sqrt{10}}{5}$, 试求此时 $\lambda$ 的值.
$5 \mathrm{G}$ 技术对社会和国家十分重要. 从战略地位来看, 业界一般将其定义为继蒸汽机革命、电 宄革命和计算机革命后的第四次工业革命. 某科技集团生产 $A, B$ 两种 $5 \mathrm{G}$ 通信基站核心部件, 下表统计了该科技集团近几年来在 $A$ 部件上的研发投人 $x$ (亿元) 与收益 $y$ (亿元) 的数据,结果如下:

(1)利用样本相关系数 $r$ 说明是否可以用线性回归模型拟合 $y$ 与 $x$ 的关系 $($ 当 $|r| \in$ $[0.75,1]$ 时, 可以认为两个变量有很强的线性相关性);
(2)求出 $y$ 关于 $x$ 的经验回归方程,并利用该方程回答下列问题:
( i ) 若要使生产 $A$ 部件的收益不低于 15 亿元, 估计至少需要投人多少研发资金?(精确 到 0.001 亿元)
( ii) 该科技集团计划用 10 亿元对 $A, B$ 两种部件进行投资,对 $B$ 部件投资 $x(1 \leqslant x \leqslant 6)$ 亿 元所获得的收益 $y$ 近似满足 $y=0.9 x-\frac{4}{x^2}+3.7$, 则该科技集团针对 $A, B$ 两种部件各应投人多 少研发资金,能使所获得的总收益 $P$ 最大.
附: 样本相关系数 $r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \sqrt{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}$, 回归直线方程的斜率 $\hat{b}=$ $\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}$, 截距 $\hat{a}=\bar{y}-\hat{b} \bar{x}$.
已知直线 $l: x=\frac{1}{2}$ 与点 $F(2,0)$, 过直线 $l$ 上的一动点 $Q$ 作直线 $P Q \perp l$, 且点 $P$ 满足 $(\overrightarrow{P F}+$ $2 \overrightarrow{P Q}) \cdot(\overrightarrow{P F}-2 \overrightarrow{P Q})=0$.
(1) 求点 $P$ 的轨迹 $C$ 的方程;
(2) 过点 $F$ 作直线与 $C$ 交于 $A, B$ 两点, 设 $M(-1,0)$, 直线 $A M$ 与直线 $l$ 相交于点 $N$. 试 问: 直线 $B N$ 是否经过 $x$ 轴上一定点? 若过定点, 求出该定点坐标; 若不过定点, 请说明理由.
已知函数 $f(x)=\frac{x}{\mathrm{e}^{x+1}}+a \ln (x+1)$.
(1) 当 $a=2$ 时, 求曲线 $y=f(x)$ 在点 $(0, f(0))$ 处的切线方程;
(2) 若函数 $f(x)$ 在 $(-1,0)$ 与 $(0,+\infty)$ 上各有一个零点, 求实数 $a$ 的取值范围.