单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $A=\left\{x\left|x^2-x-6 < 0\right|, B=|x| 2 x+3>0\right\}$, 则 $A \cap B=$
$\text{A.}$ $\left(-2,-\frac{3}{2}\right)$
$\text{B.}$ $\left(\frac{3}{2}, 3\right)$
$\text{C.}$ $\left(-\frac{3}{2}, 3\right)$
$\text{D.}$ $\left(-\frac{3}{2}, 2\right)$
若复数 $\frac{a+3 \mathrm{i}}{2+\mathrm{i}}$ 是纯虚数, 则实数 $a=$
$\text{A.}$ $-\frac{3}{2}$
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ $-\frac{2}{3}$
$\text{D.}$ $\frac{2}{3}$
已知 $\sin \left(\alpha+\frac{\pi}{3}\right)=\frac{3}{5}$, 则 $\sin \left(2 \alpha+\frac{\pi}{6}\right)=$
$\text{A.}$ $\frac{24}{25}$
$\text{B.}$ $-\frac{24}{25}$
$\text{C.}$ $\frac{7}{25}$
$\text{D.}$ $-\frac{7}{25}$
正六边形 $A B C D E F$ 中, 用 $\overrightarrow{A C}$ 和 $\overrightarrow{A E}$ 表示 $\overrightarrow{C D}$, 则 $\overrightarrow{C D}=$
$\text{A.}$ $-\frac{2}{3} \overrightarrow{A C}+\frac{1}{3} \overrightarrow{A E}$
$\text{B.}$ $-\frac{1}{3} \overrightarrow{A C}+\frac{2}{3} \overrightarrow{A E}$
$\text{C.}$ $-\frac{2}{3} \overrightarrow{A C}+\frac{2}{3} \overrightarrow{A E}$
$\text{D.}$ $-\frac{1}{3} \overrightarrow{A C}+\frac{1}{3} \overrightarrow{A E}$
"中国剩余定理" 又称 "孙子定理",1852 年英国来华传教士伟烈亚力将 《孙子算经》中 "物 不知数" 问题的解法传至欧洲. 1874 年英国数学家马西森指出此法符合 1801 年由高斯得出的 关于同余式解法的一般性定理,因而西方称之为 “中国剩余定理",“中国剩余定理" 讲的是一 个关于同余的问题.现有这样一个问题 : 将正整数中能被 3 除余 1 且被 2 除余 1 的数按由小到大 的顺序排成一列,构成数列 $\left\{a_n\right\}$ ,则 $a_{10}=$
$\text{A.}$ 55
$\text{B.}$ 49
$\text{C.}$ 43
$\text{D.}$ 37
设抛物线 $y^2=6 x$ 的焦点为 $F$, 准线为 $l, P$ 是抛物线上位于第一象限内的一点, 过 $P$ 作 $l$ 的垂线, 垂足为 $Q$, 若直线 $Q F$ 的倾斜角为 $120^{\circ}$, 则 $|P F|=$
$\text{A.}$ 3
$\text{B.}$ 6
$\text{C.}$ 9
$\text{D.}$ 12
阅读下段文字: “已知 $\sqrt{2}$ 为无理数,若 $(\sqrt{2})^{\sqrt{2}}$ 为有理数,则存在无理数 $a=b=\sqrt{2}$ ,使 得 $a^b$ 为有理数;若 $(\sqrt{2})^{\sqrt{2}}$ 为无理数,则取无理数 $a=(\sqrt{2})^{\sqrt{2}} , b=\sqrt{2}$ ,此时 $a^b=\left((\sqrt{2})^{\sqrt{2}}\right)^{\sqrt{2}}=(\sqrt{2})^{\sqrt{2} \cdot \sqrt{2}}=(\sqrt{2})^2=2$ 为有理数." 依据这段文字可以证明的结论是
$\text{A.}$ $(\sqrt{2})^{\sqrt{2}}$ 是有理数
$\text{B.}$ $(\sqrt{2})^{\sqrt{2}}$ 是无理数
$\text{C.}$ 存在无理数 $a, b$ ,使得 $a^b$ 为有理数
$\text{D.}$ 对任意无理数 $a, b$ ,都有 $a^b$ 为无理数
已知直线 $y=k x+t$ 与函数 $y=A \sin (\omega x+\varphi)(A>0, \omega>0)$ 的图象恰有两个切点, 设满足 条件的 $k$ 所有可能取值中最大的两个值分别为 $k_1$ 和 $k_2$, 且 $k_1>k_2$, 则
$\text{A.}$ $\frac{k_1}{k_2}>\frac{7}{3}$
$\text{B.}$ $\frac{5}{3} < \frac{k_1}{k_2} < \frac{7}{3}$
$\text{C.}$ $\frac{7}{5} < \frac{k_1}{k_2} < \frac{5}{3}$
$\text{D.}$ $\frac{k_1}{k_2} < \frac{7}{5}$
多选题 (共 4 题 ),每题有多个选项正确
某市 2022 年经过招商引资后,经济收入较前一年增加了一倍,实现翻番,为更好地了解 该市的经济收入的变化情况 ,统计了该市招商引资前后的年经济收入构成比例,得到如下扇形 图:

则下列结论中正确的是
$\text{A.}$ 招商引资后,工资性收人较前一年增加
$\text{B.}$ 招商引资后,转移净收人是前一年的 1.25 倍
$\text{C.}$ 招商引资后, 转移净收人与财产净收人的总和超过了该年经济收人的 $\frac{2}{5}$
$\text{D.}$ 招商引资后, 经营净收人较前一年增加了一倍
椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的一个焦点和一个顶点在圆 $x^2+y^2-5 x-4 y+4=0$ 上, 则 该椭圆的离心率的可能取值有
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{2 \sqrt{5}}{5}$
$\text{D.}$ $\frac{\sqrt{5}}{5}$
函数 $y=\left(k x^2+1\right) \mathrm{e}^x$ 的图象可能是
$\text{A.}$ 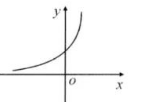 $\text{B.}$
$\text{B.}$ 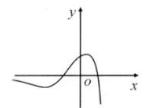 $\text{C.}$
$\text{C.}$ 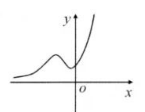 $\text{D.}$
$\text{D.}$ 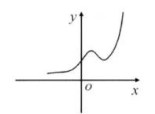
三棱锥 $P-A B C$ 中, $A B=2 \sqrt{2}, B C=1, A B \perp B C$, 直线 $P A$ 与平面 $A B C$ 所成的角为 $30^{\circ}$, 直线 $P B$ 与平面 $A B C$ 所成的角为 $60^{\circ}$, 则下列说法中正确的有
$\text{A.}$ 三棱雉 $P-A B C$ 体积的最小值为 $\frac{\sqrt{3}}{3}$
$\text{B.}$ 三棱锥 $P-A B C$ 体积的最大值为 $\frac{\sqrt{6}}{2}$
$\text{C.}$ 直线 $P C$ 与平面 $A B C$ 所成的角取到最小值时, 二面角 $P-B C-A$ 的平面角为锐角
$\text{D.}$ 直线 $P C$ 与平面 $A B C$ 所成的角取到最小值时, 二面角 $P-A B-C$ 的平面角为钝角
填空题 (共 4 题 ),请把答案直接填写在答题纸上
$(x-1)(2 x+1)^6$ 的展开式中含 $x^2$ 项的系数为
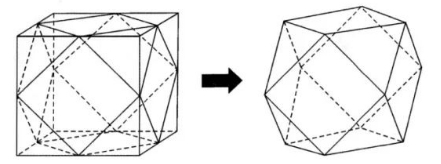
半正多面体亦称“阿基米德体”, 是以边数不全相同的正多边形为面的多面体. 如图, 将正方体沿交于一顶点的三条棱的中点截去一个三棱雉,如此共可截去八个三棱雉, 得到一个有十四个面的半正多面体, 它的各棱长都相等, 其中八个面为正三角形,六个 面为正方形,称这样的半正多面体为二十四等边体.
则得到的二十四等边体与原正方体的体积之比为
直线 $l_1: y=2 x$ 和 $l_2: y=k x+1$ 与 $x$ 轴围成的三角形是等腰三角形, 写出满足条件的 $k$ 的 两个可能取值: 利 . (写对一个得 3 分, 写对两个得 5 分)
在同一平面直角坐标系中, $P, Q$ 分别是函数 $f(x)=a x \mathrm{e}^x-\ln (a x)$ 和 $g(x)=\frac{2 \ln (x-1)}{x}$
图象上的动点, 若对任意 $a>0$, 有 $|P Q| \geqslant m$ 恒成立, 则实数 $m$ 的最大值为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
记数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 对任意 $n \in \mathbf{N}^*$, 有 $S_n=n\left(a_n+n-1\right)$.
(1) 证明: $\left\{a_n \mid\right.$ 是等差数列;
(2) 若当且仅当 $n=7$ 时, $S_n$ 取得最大值, 求 $a_1$ 的取值范围.
设 $\triangle A B C$ 的内角 $A, B, C$ 所对的边分别为 $a, b, c$, 且有 $2 \sin \left(B+\frac{\pi}{6}\right)=\frac{b+c}{a}$.
(1) 求角 $A$;
(2) 若 $B C$ 边上的高 $h=\frac{\sqrt{3}}{4} a$, 求 $\cos B \cos C$.
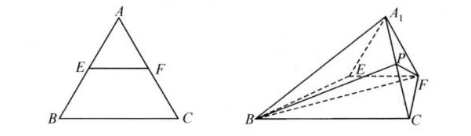
如图, 在边长为 4 的正三角形 $A B C$ 中, $E, F$ 分别为边 $A B, A C$ 的中点. 将 $\triangle A E F$ 沿 $E F$ 翻 折至 $\triangle A_1 E F$, 得到四棱锥 $A_1-E F C B, P$ 为 $A_1 C$ 的中点.
(1) 证明: $F P / /$ 平面 $A_1 B E$;
(2) 若平面 $A_1 E F \perp$ 平面 $E F C B$, 求直线 $A_1 F$ 与平面 $B F P$ 所成的角的正弦值.
中学阶段, 数学中的“对称性”不仅体现在平面几何、立体几何、解析几何和函数图象 中, 还体现在概率问题中. 例如, 甲乙两人进行比赛, 若甲每场比赛获胜概率均为 $\frac{1}{2}$, 且 每场比赛结果相互独立, 则由对称性可知, 在 5 场比赛后, 甲获胜次数不低于 3 场的概 率为 $\frac{1}{2}$. 现甲乙两人分别进行独立重复试验,每人抛掷一枚质地均匀的硬币.
(1) 若两人各抛掷 3 次, 求抛掷结果中甲正面朝上次数大于乙正面朝上次数的概率;
(2) 若甲抛掷 $(n+1)$ 次, 乙抛掷 $n$ 次, $n \in \mathbf{N}^*$, 求抛掷结果中甲正面朝上次数大于乙正 面朝上次数的概率.
过点 $(4,2)$ 的动直线 $l$ 与双曲线 $E: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 交于 $M, N$ 两点, 当 $l$ 与 $x$ 轴
平行时, $|M N|=4 \sqrt{2}$, 当 $l$ 与 $y$ 轴平行时, $|M N|=4 \sqrt{3}$.
(1) 求双曲线 $E$ 的标准方程;
(2) 点 $P$ 是直线 $y=x+1$ 上一定点, 设直线 $P M, P N$ 的斜率分别为 $k_1, k_2$, 若 $k_1 k_2$ 为定 值, 求点 $P$ 的坐标.
已知函数 $f(x)=x \ln x-\frac{k}{x}$, 其中 $k>0$.
(1) 证明: $f(x)$ 恒有唯一零点;
(2) 记 (1) 中的零点为 $x_0$, 当 $0 < k < \frac{\mathrm{e}}{2}$ 时, 证明: $f(x)$ 图象上存在关于点 $\left(x_0, 0\right)$ 对称的
两点.