江西省2025届高三第一次大联考数学试题及答案

导出试卷

江西省2025届高三第一次大联考数学试题及答案

一、单选题（共 8 题），每题只有一个选项正确

1. 已知集合

M = {x ∣ y = \lg (2 x - 3)}, N = {y ∣ y > 1}

, 则

M \cap N =

A.

(- 1, \frac{3}{2})

B.

(1, \frac{3}{2})

C.

(1, + \infty)

D.

(\frac{3}{2}, + \infty)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 某高中为鼓励全校师生增强身体素质，推行了阳光校园跑的措施，随机调查 7 名同学在某周周日校园跑的时长 (单位：分钟），得到统计数据如下：

35, 30, 50, 90, 70, 85, 60

则该组数据的中位数和平均数分别为

A.

60,58

B.

60,60

C.

55, 58

D.

55,60

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 已知

z = \frac{a + i}{1 + i} (a \in R)

为实数, 则

| 2 z + z i | =

A.

\sqrt{3}

B.

C.

D.

\sqrt{5}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 曲线

y = e^{x} + \sin 2 x

在点

(0, 1)

处的切线方程为

A.

3 x + 2 y - 2 = 0

B.

2 x - 2 y + 1 = 0

C.

3 x - y + 1 = 0

D.

3 x - 2 y + 2 = 0

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 已知锐角

α, β

满足

\sin α + \sin α \sin β = \cos α \cos β

, 则

2 α + β =

A.

\frac{π}{2}

B.

\frac{π}{3}

C.

\frac{π}{4}

D.

π

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 过点

P (1, - 3)

的直线

l

与曲线

M : (x - 2)^{2} + y^{2} = 1 (2 ⩽ x ⩽ 3)

有两个交点, 则直线

l

斜率的取值范围为

A.

(\frac{2}{3}, 1]

B.

(\frac{4}{3}, 2]

C.

(\frac{2}{3}, 2]

D.

(\frac{2}{3}, 4]

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 已知椭圆

T : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)

的右焦点为

F

, 过

F

且斜率为 1 的直线

l

与

T

交于

A, B

两点, 若线段

A B

的中点

M

在直线

x + 2 y = 0

上, 则

T

的离心率为

A.

\frac{\sqrt{2}}{4}

B.

\frac{\sqrt{5}}{3}

C.

\frac{\sqrt{3}}{5}

D.

\frac{\sqrt{2}}{2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

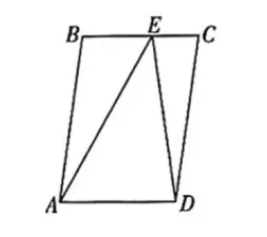
8. 如图, 在平行四边形

A B C D

中,

\tan ∠ B A D = 7, A B = 5 \sqrt{2}, A D = 5, E

为边

B C

上异于端点的一点, 且

\vec{A E} \cdot \vec{D E} = 45

, 则

\sin ∠ C D E =

A.

\frac{\sqrt{2}}{10}

B.

\frac{7}{25}

C.

\frac{5}{13}

D.

\frac{1}{4}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、多选题（共 3 题），每题有多个选项正确

9. 已知双曲线

C : \frac{x^{2}}{3 - m} - \frac{y^{2}}{m + 6} = 1

, 则

A.

m

的取值范围是

(- 6, 3)

B.

m = 1

时,

C

的渐近线方程为

y = \pm \frac{\sqrt{7}}{2} x

C.

C

的焦点坐标为

(- 3, 0), (3, 0)

D.

C

可以是等轴双曲线

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 下列函数中, 存在数列

{a_{n}}

使得

a_{1}, a_{2}, a_{3}

和

f (a_{1}), f (a_{2}), f (a_{3})

都是公差不为 0 的等差数列的是

A.

f (x) = \tan x

B.

f (x) = \log_{2} x

C.

f (x) = x^{2024}

D.

f (x) = \lg \frac{1 + x}{1 - x}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

11. 已知定义在

R

上的偶函数

f (x)

和奇函数

g (x)

满足

f (2 + x) + g (- x) = 1

, 则

A.

f (x)

的图象关于点

(2, 1)

对称

B.

f (x)

是以 8 为周期的周期函数

C.

g (x + 8) = g (x)

D.

\sum_{k = 1}^{2024} f (4 k - 2) = 2025

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、填空题（共 3 题），请把答案直接填写在答题纸上

12. 二项式

(x - y)^{6}

的展开式中

x^{4} y^{2}

的系数为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

13. 已知函数

f (x) = 2024 \sin (2 x - \frac{π}{6})

在区间

(\frac{π}{6}, m)

内恰有两个极值点，则实数

m

的取值范围为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 已知三个正整数的和为 8 , 用

X

表示这三个数中最小的数, 则

X

的期望

E X =

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

四、解答题（共 5 题），解答过程应写出必要的文字说明、证明过程或演算步骤

15. 2024 年全国田径冠军赛暨全国田径大奖赛总决赛于 6 月 30 日在山东省日照市落幕.四川田径队的吴艳妮以 12 秒 74 分的成绩打破了 100 米女子跨栏的亚洲纪录, 并夺得了 2024 年全国田径冠军赛女子 100 米跨栏决赛的冠军, 通过跑道侧面的高清轨道掫像机记录了该运动员时间

x

(单位: s ) 与位移

y

(单位: m ) 之间的关系, 得到如下表数据:

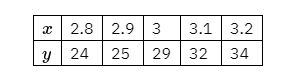
画出散点图观察可得

x

与

y

之间近似为线性相关关系.
(1) 求出

y

关于

x

的线性回归方程;
(2) 记

{\hat{e}}_{i} = y_{i} - {\hat{y}}_{i} = y_{i} - \hat{b} x_{i} - \hat{a}

, 其中

y_{i}

为观测值,

{\hat{y}}_{i}

为预测值,

{\hat{e}}_{i}

为对应

(x_{i}, y_{i})

的残差, 求前 3 项残差的和。

参考数据:

\sum_{i = 1}^{5} x_{i}^{2} = 45.1, \sum_{i = 1}^{5} x_{i} y_{i} = 434.7

, 参考公式:

\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \overset{―}{x y}}{\sum_{i = 1}^{n} x_{i}^{2} - n \overset{―}{x^{2}}}, \hat{a} = \bar{y} - \hat{b} \bar{x}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

16. 已知

A B C

的内角

A, B, C

的对边分别为

a, b, c

, 且

b = \frac{4 c \cos A}{4 - a}

.
(1) 证明:

b = 4 \cos C

;
(2) 若

C = \frac{π}{6}, c = \sqrt{3}

, 求

△ A B C

的周长.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

17. 已知直线

l : x = m y + n

交抛物线

C : y^{2} = 4 x

于

M, N

两点,

F

为

C

的焦点, 且

F M ⊥ F N

.
(1) 证明:

m^{2} + n > 0

;
(2) 求

n

的取值范围.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

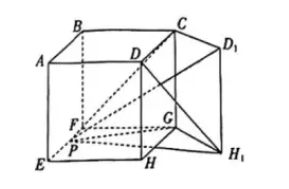
18. 如图, 在棱长为 4 的正方体

A B C D - E F G H

中, 将侧面

C D H G

沿

C G

逆时针旋转角度

θ

至平面

C D_{1} H_{1} G

, 其中

θ \in (0, \frac{π}{2})

, 点

P

是线段

E F

的中点.
(1) 当

\tan ∠ D_{1} P H_{1} = \frac{2}{3}

时, 求四棱锥

P - C D_{1} H_{1} G

的体积;
(2) 当直线

D H_{1}

与平面

C D_{1} H_{1} G

所成的角为

\frac{π}{6}

时, 求

\cos θ

的值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 定义: 若对于任意

n \in N^{*}

, 数列

{x_{n}}, {y_{n}}

满足: (1)

x_{n} \neq y_{n}

; (2)

f (x_{n}) = f (y_{n})

, 其中

f (x)

的定义域为

D, x_{n}, y_{n} \in D

, 则称

{x_{n}}, {y_{n}}

关于

f (x)

满足性质

G

.
(1) 请写出一个定义域为

R

的函数

f (x)

, 使得

{n}, {- n}

关于

f (x)

满足性质

G

;
(2) 设

g (x) = x + \frac{k}{x} (x > 0, k > 0)

, 若

{x_{n}}, {y_{n}}

关于

g (x)

满足性质

G

, 证明:

x_{n} + y_{n} > 2 \sqrt{k}

；
(3) 设

h (x) = e^{\frac{π}{2} + x} + e^{- \frac{π}{2} x} - \sin x (x \in R)

, 若

{x_{n}}, {y_{n}}

关于

h (x)

满足性质

G

, 求数列

{x_{n} + y_{n}}

的前

n

项和。

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。