单选题 (共 10 题 ),每题只有一个选项正确
关于 $x$ 的一元二次方程 $4 x^2-2 x-5=0$ 的根的情况是
$\text{A.}$ 有两个不相等的实数根
$\text{B.}$ 有两个相等的实数根
$\text{C.}$ 没有实数根
$\text{D.}$ 无法判断
下列图形,可以看作是中心对称图形的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
抛物线 $y=x^2-2 x+3$ 的对称轴是直线
$\text{A.}$ $x=-2$
$\text{B.}$ $x=3$
$\text{C.}$ $x=-1$
$\text{D.}$ $x=1$
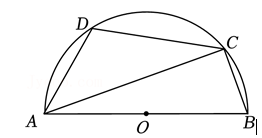
如图, $A B$ 是半圆 $O$ 的直径, $C, D$ 是半圆上的两点, 若 $\angle B A C=20^{\circ}$. 则 $\angle D$ 的大小为
$\text{A.}$ $100^{\circ}$
$\text{B.}$ $110^{\circ}$
$\text{C.}$ $120^{\circ}$
$\text{D.}$ $130^{\circ}$
已知二次函数 $y=(k-3) x^2+2 x+1$ 的图像与 $x$ 轴有交点, 则 $k$ 的取值范围是
$\text{A.}$ $k < 4$
$\text{B.}$ $k \leqslant 4$ 且 $k \neq 3$
$\text{C.}$ $k>4$
$\text{D.}$ $k \leqslant 4$
已知二次函数 $y=a x^2+b x+c$ 中, 函数 $y$ 与自变量 $x$ 的部分对应值如下表:

若点 $P\left(\frac{\mathrm{m}^2}{4}+1, y_1\right), Q\left(m-1, y_2\right)$ 都在该函数图象上, 则 $y_1$ 和 $y_2$ 的大小关系是
$\text{A.}$ $y_1 < y_2$
$\text{B.}$ $y_1>y_2$
$\text{C.}$ $y_1 \leqslant y_2$
$\text{D.}$ $y_1 \geqslant y_2$
圆的直径是 14 , 若圆心与直线上某一点的距离是 7 , 则该直线和圆的位置关系是
$\text{A.}$ 相离
$\text{B.}$ 相切
$\text{C.}$ 相交
$\text{D.}$ 相交或相切
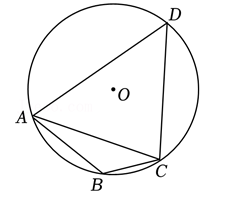
如图, 四边形 $A B C D$ 内接于 $\odot O, \angle A B C=135^{\circ}, A C=4$, 则 $\odot O$ 的半径为
$\text{A.}$ $4$
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ $2 \sqrt{3}$
$\text{D.}$ $4 \sqrt{2}$
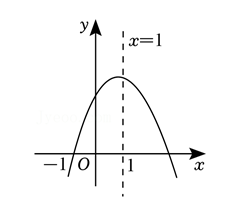
如图是二次函数 $y=a x^2+b x+c(a \neq 0)$ 的图像, 则下列结论正确的有
(1) $a b c>0$;
(2) $2 a+b=0$;
(3) $b^2 < 4 a c$;
(4) $4 a+2 b+c>0$;
(5) $a+b \geqslant a m^2+b m$ ( $m$ 为任意实数)
$\text{A.}$ 2个
$\text{B.}$ 3个
$\text{C.}$ 4个
$\text{D.}$ 5个
已知抛物线 $y=-(x-a)^2+a-1$ ( $a$ 为常数), 则下列判断正确的是
(1)当 $-1 < x < 2$ 时, $y$ 随 $x$ 的增大而增大, 则 $a$ 的取值范围为 $a \geqslant 2$;
(2)无论 $a$ 为何值, 该抛物线的顶点始终在一条直线上
$\text{A.}$ 两个都对
$\text{B.}$ 两个都错
$\text{C.}$ 只有(1)对
$\text{D.}$ 只有(2)对
填空题 (共 7 题 ),请把答案直接填写在答题纸上
抛物线 $y=a x^2-2 x-1$ 与 $x$ 轴有唯一一个交点, 则 $a$ 的值为
关于 $x$ 的一元二次方程 $(a-2) x^2-4 x+1=0$ 有实数根, 则 $a$ 的取值范围是
已知二次函数 $y=(m+1) x^{m^2-1}$ 的图象开口向下, 则 $m$ 的值是
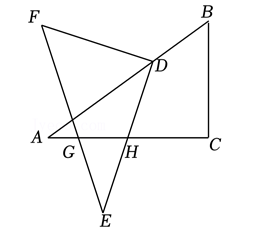
如图, 将 Rt $\triangle A B C$ 绕直角边 $A C$ 的中点 $H$ 旋转, 得到 $\triangle E F D$. 若 $\triangle E F D$ 的直角顶点 $D$ 落在 $\triangle A B C$ 的斜边 $A B$ 上, $E F$ 与 $A C$ 交于点 $G$, 且 $\triangle E G H$ 恰好是以 $G H$ 为底边的等腰三 角形, 则 $\angle A=$
若点 $A\left(3, y_1\right), B\left(-5, y_2\right), C\left(7, y_3\right)$ 为二次函数 $y=(x+2){ }^2-9$ 的图象上的三 点, 则 $y_1, y_2, y_3$ 的大小关系是
某初三学生对自己某次实心球训练时不慎脱手, 发现实心球飞行高度 $y$ (米) 与水平距 离 $x$ (米) 之间的关系为 $y=\frac{1}{12} x^2-\frac{2}{3} x+\frac{5}{3}$, 由此可知该考生此次实心球训练的成绩为 ( ) 米.
一辆宽为 $2 m$ 的货车要通过跨度为 $8 m$, 拱高为 $4 m$ 的截面为抛物线的单行隧道 (从正中 间通过), 抛物线满足关系式 $y=\frac{1}{4} x^2+4$. 为保证安全, 车顶离隧道至少要有 $0.5 m$ 的距 离, 则货车的限高应为 ( ) $m$.
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知二次函数 $y=a x^2-4 a x+4$ 的图像与 $x$ 轴有唯一公共点.
(1) 求 $a$ 的值;
(2) 当 $0 \leqslant x \leqslant m$ 时 $(m>0)$, 函数的最大值为 4 , 且最小值为 0 , 则实数 $m$ 的取值范围 是
(1) 解方程: $x^2-5 x+3=0$;
(2) $2 x^2+6=7 x$ (配方法)
(3) 已知关于 $x$ 的方程 $2 x^{2}+(k-2) x+1=0$ 有两个相等的实数根, 求 $k$ 的值.
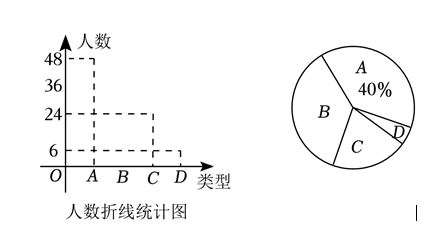
某校的学生除了体育课要进行体育锻炼外, 寒暑假期间还要自己抽时间进行体育锻炼, 为了 了解同学们假期体育锻炼的情况, 开学时体貟老师随机抽取了部分同学进行调查, 按锻 炼的时间 $x$ (分钟) 分为以下四类: $A$ 类 $(0 \leqslant x \leqslant 15), B$ 类 $(15 < x \leqslant 30), C$ 类 $(=$ $\left.\sin \left(x-\frac{\pi}{6}\right)+\frac{1}{2}\right), D$ 类 $(x>45)$, 对调查结果进行整理并绘制了如图所示的不完整的 折线统计图和扇形统计图, 请结合图中的信息解答下列各题:
(1) 扇形统计图中 $D$ 类所对应的圆心角度数为 , 并补全折线统计图;
(2) 现从 $A$ 类中选出两名男同学和三名女同学, 从以上五名同学中随机抽取两名同学进 行采访, 请利用画树状图或列表的方法求出抽到的学生恰好是一男一女的概率.
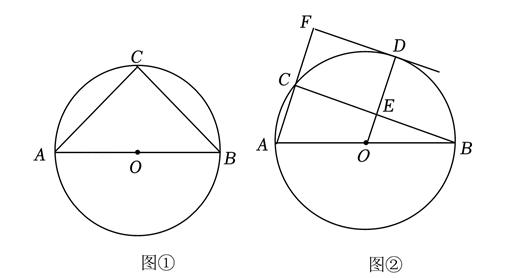
已知 $A B$ 为 $\odot O$ 的直径, $A B=8, C$ 为 $\odot O$ 上一点, 连接 $C A, C B$.
(I) 如图(1), 若 $C$ 为 $A B$ 的中点, 求 $\angle C A B$ 的大小和 $A C$ 的长;
(II) 如图(2), 若 $A C=2, O D$ 为 $\odot O$ 的半径, 且 $O D \perp C B$, 垂足为 $E$, 过点 $D$ 作 $\odot O$ 的 切线, 与 $A C$ 的延长线相交于点 $F$, 求 $F D$ 的长.
随着疫情的持续, 各地政府储存了充足的防疫物品. 某防疫物品储藏室的截面是由如图所 示的图形构成的, 图形下面是长方形 $A B C D$, 上面是半圆形, 其中 $A B=2.3 m, B C=2.6 m$, 一辆装满货物的运输车, 其外形高 $2.6 m$, 宽 $2.4 m$, 它能通过储藏室的门吗? 请说明理由.

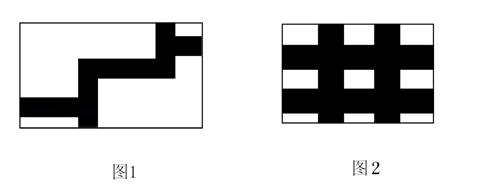
(1) 如图 1, 在一块长为 $40 \mathrm{~m}$, 宽为 $30 \mathrm{~m}$ 的矩形地面上, 修建有道路, 道路都是等宽的, 剩余部分种上草坪, 测得草坪的面积是 $1064 m^2$, 道路的宽度是多少?
(2) 后来要在这块长为 $40 m$, 宽为 $30 m$ 的矩形地面上, 进行重新规划, 打算修建两横两 坚的道路(横坚道路各与矩形的一条边平行), 如图 2, 横、坚道路的宽度相同, 剩余部 分种上草坪, 如果要使草坪的面积是地面面积的二分之一, 应如何设计道路的宽度?
如图 1, 在平面直角坐标系中, 抛物线 $y=a x^2+b x-3$ 与 $x$ 轴交于点 $A(6,0), B(-1$, 0 ), 与 $y$ 轴交于点 $C$, 连接 $B C$, 过点 $A 、 C$ 作直线 $A C$.
(1) 求抛物线的函数解析式.
(2) 点 $P$ 为直线 $A C$ 下方抛物线上一动点, 过点 $P$ 作 $P F \perp A C$ 交 $A C$ 于点 $F$, 过点 $P$ 作 $P E / / A C$ 交 $x$ 轴于点 $E$, 求 $A E+P F$ 的最大值及此时点 $P$ 的坐标.
(3) 在 (2) 问的条件下, 将抛物线 $y=a x^2+b x-3$ 沿射线 $C B$ 方向平移 $\sqrt{10}$ 个单位长度 得到新抛物线 $y^{\prime}$, 新抛物线 $y^{\prime}$ 与原抛物线交于点 $M$; 连接 $C P$, 把线段 $C P$ 沿直线 $A C$ 平 移, 记平移后的线段为 $C P^{\prime}$, 当以 $C 、 P^{\prime} 、 M$ 为顶点的三角形是等腰三角形时, 请直接 写出所有符合条件的 $P^{\prime}$ 点的坐标.
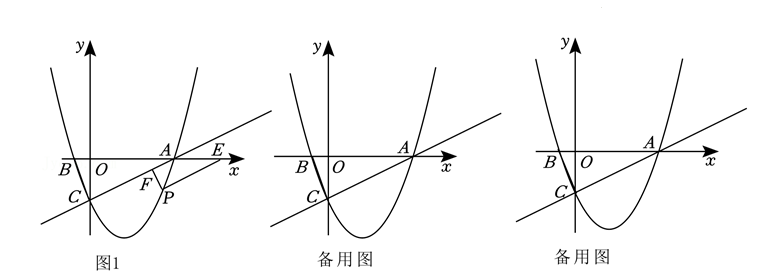
如图 1, 已知抛物线 $F_l: y=-x^2+2 x+3$ 交 $x$ 轴于 $A 、 B$ 两点, 与 $y$ 轴交于点 $C$, 抛物 $F_2: y$ $=\frac{1}{2} x^2+b x+c$ 经过点 $A 、 B$, 点 $P$ 是射线 $C B$ 上一动点.
(1) 求抛物线 $F_2$ 和直线 $B C$ 的函数表达式.
(2) 如图 2, 过点 $P$ 作 $P E$ 上 $B C$ 交抛物线 $F_l$ 第一象限部分于点 $E$, 作 $E F / / A B$ 交 $B C$ 于 点 $F$, 求 $\triangle P E F$ 面积的最大值及此时点 $E$ 的坐标.
(3) 抛物线 $F_l$ 与 $F_2$ 在第一象限内的图象记为 “图象 $Z$ ”, 过点 $P$ 作 $P G / / y$ 轴交图象 $Z$ 于点 $G$, 是否存在这样的点 $P$, 使 $\triangle C P G$ 与 $\triangle O B C$ 相似? 若存在, 求出所有符合条件的 点 $P$ 的横坐标.