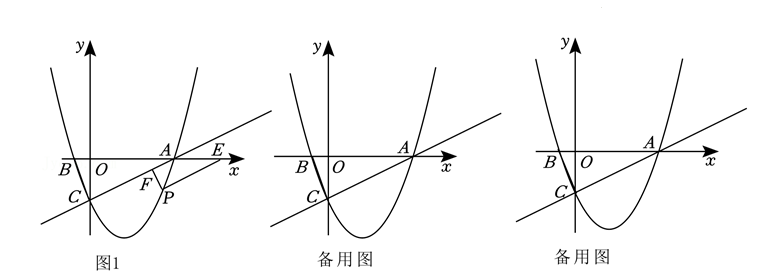
如图 1, 在平面直角坐标系中, 抛物线 $y=a x^2+b x-3$ 与 $x$ 轴交于点 $A(6,0), B(-1$, 0 ), 与 $y$ 轴交于点 $C$, 连接 $B C$, 过点 $A 、 C$ 作直线 $A C$.
(1) 求抛物线的函数解析式.
(2) 点 $P$ 为直线 $A C$ 下方抛物线上一动点, 过点 $P$ 作 $P F \perp A C$ 交 $A C$ 于点 $F$, 过点 $P$ 作 $P E / / A C$ 交 $x$ 轴于点 $E$, 求 $A E+P F$ 的最大值及此时点 $P$ 的坐标.
(3) 在 (2) 问的条件下, 将抛物线 $y=a x^2+b x-3$ 沿射线 $C B$ 方向平移 $\sqrt{10}$ 个单位长度 得到新抛物线 $y^{\prime}$, 新抛物线 $y^{\prime}$ 与原抛物线交于点 $M$; 连接 $C P$, 把线段 $C P$ 沿直线 $A C$ 平 移, 记平移后的线段为 $C P^{\prime}$, 当以 $C 、 P^{\prime} 、 M$ 为顶点的三角形是等腰三角形时, 请直接 写出所有符合条件的 $P^{\prime}$ 点的坐标.