如图 1, 已知抛物线 $F_l: y=-x^2+2 x+3$ 交 $x$ 轴于 $A 、 B$ 两点, 与 $y$ 轴交于点 $C$, 抛物 $F_2: y$ $=\frac{1}{2} x^2+b x+c$ 经过点 $A 、 B$, 点 $P$ 是射线 $C B$ 上一动点.
(1) 求抛物线 $F_2$ 和直线 $B C$ 的函数表达式.
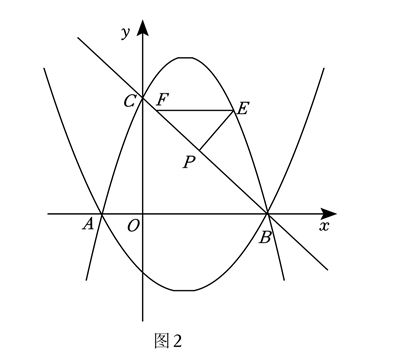
(2) 如图 2, 过点 $P$ 作 $P E$ 上 $B C$ 交抛物线 $F_l$ 第一象限部分于点 $E$, 作 $E F / / A B$ 交 $B C$ 于 点 $F$, 求 $\triangle P E F$ 面积的最大值及此时点 $E$ 的坐标.
(3) 抛物线 $F_l$ 与 $F_2$ 在第一象限内的图象记为 “图象 $Z$ ”, 过点 $P$ 作 $P G / / y$ 轴交图象 $Z$ 于点 $G$, 是否存在这样的点 $P$, 使 $\triangle C P G$ 与 $\triangle O B C$ 相似? 若存在, 求出所有符合条件的 点 $P$ 的横坐标.
(1) 求抛物线 $F_2$ 和直线 $B C$ 的函数表达式.
(2) 如图 2, 过点 $P$ 作 $P E$ 上 $B C$ 交抛物线 $F_l$ 第一象限部分于点 $E$, 作 $E F / / A B$ 交 $B C$ 于 点 $F$, 求 $\triangle P E F$ 面积的最大值及此时点 $E$ 的坐标.
(3) 抛物线 $F_l$ 与 $F_2$ 在第一象限内的图象记为 “图象 $Z$ ”, 过点 $P$ 作 $P G / / y$ 轴交图象 $Z$ 于点 $G$, 是否存在这样的点 $P$, 使 $\triangle C P G$ 与 $\triangle O B C$ 相似? 若存在, 求出所有符合条件的 点 $P$ 的横坐标.
