单选题 (共 12 题 ),每题只有一个选项正确
若集合 $A=\left\{x \mid x^2-2 x < 0\right\}, B=\left\{x \mid \log _2 x \geqslant 0\right\}$, 则图中阴影部分表示的集合为
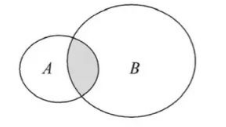
$\text{A.}$ $\{x \mid x>0\}$
$\text{B.}$ $\{x \mid 0 < x \leqslant 1\}$
$\text{C.}$ $\{x \mid 1 \leqslant x < 2\}$
$\text{D.}$ $\{x \mid 0 < x < 1$ 或 $x \geqslant 2\}$
设复数 $z=\frac{\mathrm{i}}{1+\mathrm{i}}$, 则复数 $z$ 的共轭复数 $\bar{z}$ 在复平面内对应的点位于
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
已知函数 $y=f(x)$ 的图象在点 $P(3, f(3))$ 处的切线方程是 $y=-2 x+7$, 则 $f(3)-f^{\prime}(3)=$
$\text{A.}$ $-2$
$\text{B.}$ 2
$\text{C.}$ $-3$
$\text{D.}$ 3
某高中 2022 年的高考考生人数是 2021 年高考考生人数的 $1.5$ 倍. 为了更好地对比该校考生的升学情 况, 统计了该校 2021 年和 2022 年高考分数达线情况, 得到如图所示扇形统计图:

下列结论正确的是
$\text{A.}$ 该校 2022 年与 2021 年的本科达线人数比为 $6: 5$
$\text{B.}$ 该校 2022 年与 2021 年的专科达线人数比为 $6: 7$
$\text{C.}$ 2022 年该校本科达线人数增加了 $80 \%$
$\text{D.}$ 2022 年该校不上线的人数有所减少
已知向量 $\boldsymbol{a}=(-4,-3), \boldsymbol{b}=(m, 1)$, 且夹角的余弦值为 $-\frac{3}{5}$, 则 $m=$
$\text{A.}$ 0
$\text{B.}$ $-1$
$\text{C.}$ 0 或 $-\frac{24}{7}$
$\text{D.}$ $-\frac{24}{7}$
“ $0 < x < 1$ ”是 “ $x+\frac{1}{x+1}>1$ ”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 既不充分也不必要条件
$\text{D.}$ 充要条件
我国南宋时期著名的数学家秦九韶在其著作《数书九章》中, 提出了已知三角形三边长求三角形面 积的公式, 可以看出我国古代已具有很高的数学水平. 设 $a, b, c$ 分别为 $\triangle A B C$ 内角 $A, B, C$ 的对边, $S$ 表示 $\triangle A B C$ 的面积,其公式为 $S=\sqrt{\frac{1}{4}\left[a^2 b^2-\left(\frac{a^2+b^2-c^2}{2}\right)^2\right]}$. 若 $b=\sqrt{2}, \frac{a+b+c}{\sin A+\sin B+\sin C}$ $=\frac{c}{2 \sin A}$, 则 $\triangle A B C$ 面积 $S$ 的最大值为
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $1$
$\text{C.}$ $\frac{2}{3}$
$\text{D.}$ $\frac{\sqrt{2}}{3}$
从正方体的 8 个顶点和中心中任选 4 个, 则这 4 个点恰好构成三棱锥的概率为
$\text{A.}$ $\frac{41}{63}$
$\text{B.}$ $\frac{38}{63}$
$\text{C.}$ $\frac{2}{3}$
$\text{D.}$ $\frac{5}{7}$
已知函数 $f(x)$ 的局部图象如图所示, 下列函数 $f(x)$ 的解析式与图 象符合的可能是
$\text{A.}$ $f(x)=\frac{4}{5} x^2$
$\text{B.}$ $f(x)=x^4$
$\text{C.}$ $f(x)=x \sin x$
$\text{D.}$ $f(x)=\frac{x}{x^2+1}$
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{3}=1(a>0)$ 的左、右焦点分别为 $F_1, F_2$, 离心率为 $2, P$ 为 $C$ 上一点, 则
$\text{A.}$ 双曲线 $C$ 的实轴长为 2
$\text{B.}$ 双曲线 $C$ 的一条渐近线方程为 $y=\sqrt{3} x$
$\text{C.}$ $\left|P F_1\right|-\left|P F_2\right|=2$
$\text{D.}$ 双曲线 $C$ 的焦距为 4
已知 $\left\{a_n\right\}$ 为等差数列, $S_n$ 为其前 $n$ 项和, 则下列结论一定成立的是
$\text{A.}$ 若 $a_1=a_5$, 则 $a_1=a_2=\cdots=a_n$
$\text{B.}$ 若 $a_5>a_3$, 则 $S_1 < S_2 < \cdots < S_n$
$\text{C.}$ 若 $a_3=2$, 则 $a_1^2+a_5^2 \geqslant 8$
$\text{D.}$ 若 $a_4=8, a_8=4$, 则 $S_{12}=66$
如图, 在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, 动点 $E$ 在线段 $A_1 C_1$ 上, 则
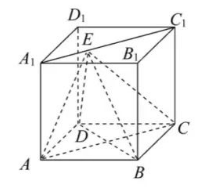
$\text{A.}$ 直线 $A_1 C_1$ 与 $B C$ 所成的角为 $30^{\circ}$
$\text{B.}$ 对任意的点 $E$, 都有 $B D \perp$ 平面 $A C E$
$\text{C.}$ 存在点 $E$, 使得平面 $A B E / /$ 平面 $C C_1 D_1 D$
$\text{D.}$ 存在点 $E$, 使得平面 $A B E \perp$ 平面 $C D E$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
若抛物线 $y^2=4 x$ 的准线与圆 $C:(x-a)^2+y^2=1$ 相切, 则 $a=$
已知 $(x+1)(x-1)^5=a_0+a_1 x+a_2 x^2+a_3 x^3+a_1 x^4+a_5 x^5+a_6 x^6$, 则 $a_0+a_3$ 的值
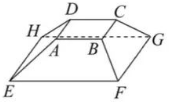
如图, 在正四棱台 $A B C D E F G H$ 中, $A B=4 \sqrt{3}, E F=9 \sqrt{3}$, 且四棱雉 $E-A B C D$ 的体积为 48 , 则该四棱台的体积为
设函数 $f(x)=\sin \omega x+\sin \left(\omega x+\frac{\pi}{3}\right)(\omega>0)$, 已知 $f(x)$ 在 $[0, \pi]$ 上有 且仅有 3 个极值点, 则 $\omega$ 的取值范围是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在① $b^2+c^2-a^2=2 \sqrt{3} a c \sin B$; ② $\sin ^2 B+\sin ^2 C-\sin ^2 A=\sqrt{3} \sin B \sin C$ 这两个条 件中任选一个, 补充在下面的问题中并作答.
在 $\triangle A B C$ 中, 内角 $A, B, C$ 所对的边分别是 $a, b, c$,
(1)求角 $A$;
(2) 若 $a=8, b+c=10$, 求 $\triangle A B C$ 的面积.
设 $S_n$ 是等比数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 且 $S_3=14, S_6=126$.
(1)求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 记 $b_n=(n-1) a_n$, 数列 $\left\{b_n\right\}$ 的前 $n$ 项和为 $T_n$, 求 $T_n$.
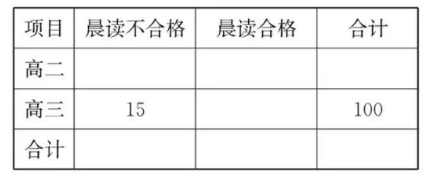
暑假期间, 某学校建议学生保持晨读的习惯, 开学后, 该校对高二、高三随 机抽取 200 名学生(该学校学生总数较多), 调查日均晨读时间, 数据如表:

将学生日均晨读时间在 $[30,60]$ 上的学生评价为“晨读合格”.
(1)请根据上述表格中的统计数据填写下面 $2 \times 2$ 列联表, 依据 $\alpha=0.05$ 的独立性检验, 能否 认为“晨读合格”与年级有关联?
(2) 将上述调查所得到的频率视为概率来估计全校的情况, 现在从该校所有学生中, 随机抽 取 2 名学生, 记所抽取的 2 人中晨读合格的人数为随机变量 $\xi$, 求 $\xi$ 的分布列和数学期望.
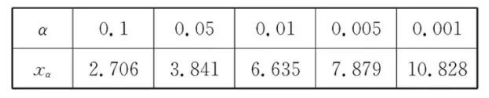
参考公式: $\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$, 其中 $n=a+b+c+d$.
参考数据:
如图,在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 为梯形, $A B=2 A D=2 D C, A B / /$ $D C, A B \perp A D$, 平面 $P C B \perp$ 平面 $A B C D$.
(1) 证明: $P B \perp A C$;
(2) 若 $\triangle P C B$ 为正三角形, 求二面角 $B P A-C$ 的正弦值.

已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别为 $F_1, F_2$, 上、顶点分 别为 $M, N, \triangle N F_1 F_2$ 的面积为 $\sqrt{3}$, 四边形 $M F_2 N F_1$ 的四条边的平方和为 16 .
(1)求椭圆 $C$ 的方程;
(2) 若 $a>b>1$, 斜率为 $k$ 的直线 $l$ 交椭圆 $C$ 于 $A, B$ 两点, 且线段 $A B$ 的中点 $H$ 在直线 $x=$ $\frac{1}{2}$ 上, 求证: 线段 $A B$ 的垂直平分线与圆 $x^2+y^2=\frac{1}{4}$ 恒有两个交点.
已知函数 $f(x)=x-a \ln x(a \neq 0)$.
(1) 讨论函数 $f(x)$ 的单调性;
(2) 若 $g(x)=x \mathrm{e}^x-a(\ln x+x)$, 且 $a>\mathrm{e}$, 证明: $g(x)$ 有且仅有两个零点. (e 为自然对数的底数)