暑假期间, 某学校建议学生保持晨读的习惯, 开学后, 该校对高二、高三随 机抽取 200 名学生(该学校学生总数较多), 调查日均晨读时间, 数据如表:

将学生日均晨读时间在 $[30,60]$ 上的学生评价为“晨读合格”.
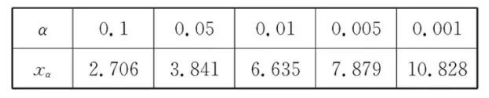
(1)请根据上述表格中的统计数据填写下面 $2 \times 2$ 列联表, 依据 $\alpha=0.05$ 的独立性检验, 能否 认为“晨读合格”与年级有关联?
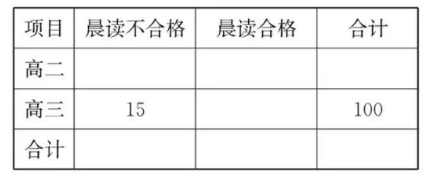
(2) 将上述调查所得到的频率视为概率来估计全校的情况, 现在从该校所有学生中, 随机抽 取 2 名学生, 记所抽取的 2 人中晨读合格的人数为随机变量 $\xi$, 求 $\xi$ 的分布列和数学期望.
参考公式: $\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$, 其中 $n=a+b+c+d$.
参考数据:

将学生日均晨读时间在 $[30,60]$ 上的学生评价为“晨读合格”.
(1)请根据上述表格中的统计数据填写下面 $2 \times 2$ 列联表, 依据 $\alpha=0.05$ 的独立性检验, 能否 认为“晨读合格”与年级有关联?

(2) 将上述调查所得到的频率视为概率来估计全校的情况, 现在从该校所有学生中, 随机抽 取 2 名学生, 记所抽取的 2 人中晨读合格的人数为随机变量 $\xi$, 求 $\xi$ 的分布列和数学期望.
参考公式: $\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$, 其中 $n=a+b+c+d$.
参考数据:
