单选题 (共 8 题 ),每题只有一个选项正确
若复数 $z=\frac{1-2 \mathrm{i}}{2+\mathrm{i}}$, 则 $\bar{z}=$
$\text{A.}$ $\mathrm{i}$
$\text{B.}$ $-\mathrm{i}$
$\text{C.}$ 1
$\text{D.}$ -1
命题 “ $\exists x>1, x>2$ ” 的否定是
$\text{A.}$ $\exists x \leq 1, x>2$
$\text{B.}$ $\exists x \leq 1, x \leq 2$
$\text{C.}$ $\forall x>1, x \leq 2$
$\text{D.}$ $\forall x>1, x>2$
已知向量 $\vec{a}=(1,2), \vec{b}=(1,-3)$, 则
$\text{A.}$ $a / /(a+b)$
$\text{B.}$ $a / /(a-b)$
$\text{C.}$ $a \perp(a-b)$
$\text{D.}$ $a \perp(a+b)$
已知数列 $\left\{a_n\right\}$ 满足 $a_1=1, a_{n+1}^2-a_n^2=2$, 则 $a_5=$
$\text{A.}$ 3
$\text{B.}$ 2 或 -2
$\text{C.}$ 3 或 -3
$\text{D.}$ 2
$\left(x^2-x+y\right)^5$ 的展开式中 $x^5 y^2$ 的系数为
$\text{A.}$ -30
$\text{B.}$ -20
$\text{C.}$ 20
$\text{D.}$ 30
设抛物线 $C: y^2=2 p x(p>0)$ 的焦点为 $F$, 过点 $F$ 且倾斜角为 $\frac{\pi}{4}$ 的直线与 $C$ 交于 $A, B$ 两点, 以 $A B$ 为直径的圆与准线 $l$ 切于点 $M\left(-\frac{p}{2}, 2\right)$, 则 $C$ 的方程为
$\text{A.}$ $y^2=2 x$
$\text{B.}$ $y^2=4 x$
$\text{C.}$ $y^2=6 x$
$\text{D.}$ $y^2=8 x$
在 $\triangle A B C$ 中, $\overrightarrow{A D}=\frac{2}{3} \overrightarrow{A B}+\frac{1}{3} \overrightarrow{A C}, \angle B A D=\theta, \angle C A D=2 \theta$, 则下列各式一定成立的是
$\text{A.}$ $\sin B=\cos \theta \sin C$
$\text{B.}$ $\sin C=\cos \theta \sin B$
$\text{C.}$ $\sin B=\sin \theta \sin C$
$\text{D.}$ $\sin C=\sin \theta \sin B$
在满足 $2 \leq x_i < y_i, x_i^{y_i}=y_i^{x_i}$ 的实数对 $\left(x_1, y_1\right)(i=1,2,3, \mathrm{~L}, n)$ 中, 使得 $y_1+y_2+\mathrm{L}+y_{n-1} \leq 15 y_n$ 成立的正整数 $n$ 的最大位为
$\text{A.}$ 15
$\text{B.}$ 16
$\text{C.}$ 22
$\text{D.}$ 23
多选题 (共 3 题 ),每题有多个选项正确
已知函数 $f(x)=\sin (\omega x+\varphi)\left(\omega>0,-\frac{\pi}{2} < \varphi < \frac{\pi}{2}\right)$ 的部分图像如图所示, 则
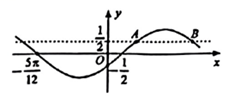
$\text{A.}$ $f(x)$ 在 $\left(0, \frac{\pi}{3}\right)$ 上单调递增
$\text{B.}$ $f(x)$ 在 $(0,6)$ 上有 4 个零点
$\text{C.}$ $|A B|=\frac{\pi}{3}$
$\text{D.}$ 将 $y=\sin x$ 的图祭向右平移 $\frac{\pi}{6}$ 个单位, 可得 $y=f(x)$ 的图集
若函数 $f(x)$ 的定义域为 $R$, 且 $f(x+y)+f(x-y)=2 f(x) f(y), f(2)=-1$, 则
$\text{A.}$ $f(0)=0$
$\text{B.}$ $f(x)$ 为偶函数
$\text{C.}$ $f(x)$ 的图象关于点 $(1,0)$ 对称
$\text{D.}$ $\sum_{i=1}^{\infty} f(i)=-1$
某广场设置了一些石凳供大家休息,这些石凳是由棱长为40cm的正方体截去八个一样的四面体得到的,则
$\text{A.}$ 该几何体的顶点数为12
$\text{B.}$ 该几何体的棱数为24
$\text{C.}$ 该几何体的表面积为$(4800+800 \sqrt{3}) cm^2$
$\text{D.}$ 该几何体外接球的表面积是原正方体内切球、外接球表面积的等差中项
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知集合 $A=\{(x, y) \mid x-y=1\}, B=\left\{(x, y) \mid(x-2)^2+(y+3)^2=9\right\}$, 则 $A \cap B$ 的子集个数为
在工业生产中轴承的直径服从 $N(3.0,0.0025)$, 购买者要求直径为 $3.0 \pm \varepsilon$, 不在这个范围的将被拒绝,要使拒绝的概率控制在 $4.55 \%$ 之内, 则 $\varepsilon$ 至少为 ________ ; (若 $X \sim N\left(\mu, \sigma^2\right)$, 则 $P(|X-\mu| < 2 \sigma)=$ 0.9545 )
设双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1, F_2, A$ 是右支上一点, 满足 $A F_1 \perp A F_2$, 直线 $A F_2$ 交双曲线于另一点 $B$, 且 $\left|B F_1\right|-\left|A F_1\right|=2 a$, 则双曲线离心率的一个值为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设等比数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 已知 $a_2+a_4=30, S_4=45$.
(I) 求 $\left\{a_n\right\}$ 的通项公式;
(II) 设 $b_n=\frac{1}{a_n a_{n+1}}$, 求 $\left\{b_n\right\}$ 的前 $n$ 项和 $T_n$.
我们平时常用的视力表叫做对数视力表, 视力呈现为 $4.8,4.9,5.0,5.1$. 视力 $\geq 5.0$ 为正常视力. 否则就是近视. 某地区对学生视力与学习成结进行调查, 随机抽查了 100 名近视学生的成绩, 得到频率分布直方图:
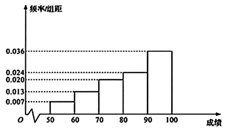
(I)能否据此判断学生的学习成绩与视力状况相关?(不需说明理由)
(II) 估计该地区近视学生学习成缆的第 85 百分位数;(精确到 0.1 )
(III) 已知该地区学生的近视率为 $54 \%$, 学生成绩的优秀率为 $36 \%$ (成绩 $\geq 85$ 分为优秀), 从该地区学生中任选一人, 若此人的成绩为优秀, 求此人近视的概率. (以样本中的频率作为相应的概率)
如图, 在四棱椎 $P-A B C D$ 中, 底面 $A B C D$ 为正方形, $P A \perp$ 平面 $A B C D, P A=A B$, 点 $E, F$ 分别是棱 $P B, B C$ 的中点.
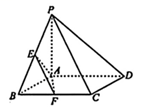
(I) 求直线 $A F$ 与平面 $P B C$ 所成角的正弦值;
(II) 在截面 $A E F$ 内是否存在点 $G$. 使 $D G \perp$ 平面 $A E F$, 并说明理由.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\frac{\sqrt{6}}{3}$, 点 $P(0,2)$ 在椭圆 $C$ 上, 过点 $P$ 的两条直线 $P A, P B$ 分别与椭圆 $C$ 交于另一点 $A, B$, 且直线 $P A, P B, A B$ 的斜率满足 $k_{P A}+k_{P B}=4 k_{A B}\left(k_{A B} \neq 0\right)$.
(I) 求椭圆 $C$ 的方程;
(II) 证明直线 $A B$ 过定点;
(III) 椭圆 $C$ 的焦点分别为 $F_1, F_2$, 求凸四边形 $F_1 A F_2 B$ 面积的取值范围.
已知函数 $f(x)=\ln x+a x^2-x+a+1$.
(I)证明曲线 $y=f(x)$ 在 $x=1$ 处的切线过原点;
(II)讨论 $f(x)$ 的单调性;
(III) 若 $f(x) \leq e^x$, 求实数 $a$ 的取值范围.