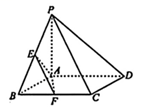
如图, 在四棱椎 $P-A B C D$ 中, 底面 $A B C D$ 为正方形, $P A \perp$ 平面 $A B C D, P A=A B$, 点 $E, F$ 分别是棱 $P B, B C$ 的中点.
(I) 求直线 $A F$ 与平面 $P B C$ 所成角的正弦值;
(II) 在截面 $A E F$ 内是否存在点 $G$. 使 $D G \perp$ 平面 $A E F$, 并说明理由.

(I) 求直线 $A F$ 与平面 $P B C$ 所成角的正弦值;
(II) 在截面 $A E F$ 内是否存在点 $G$. 使 $D G \perp$ 平面 $A E F$, 并说明理由.