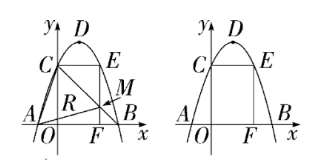10道经典中考数学压轴题

导出试卷

10道经典中考数学压轴题

解答题（共 10 题），解答过程应写出必要的文字说明、证明过程或演算步骤

已知二次函数的解析式为 $y=-x^2+4 x$, 该二次函数交 $x$ 轴于 $O 、 B$ 两点, $A$ 为抛物线上一点, 且横纵坐标相等(原点除外), $P$ 为二次函数上一动点, 过 $P$ 作 $x$ 轴垂线, 垂足为 $D(a, 0)(a>0)$,并与直线 $O A$ 交于点 $C$.
(1)求 $A 、 B$ 两点的坐标;
(2)当点 $P$ 在线段 $O A$ 上方时，过 $P$ 作 $x$ 轴的平行线与线段 $O A$相交于点 $E$, 求 $\triangle P C E$ 周长的最大值及此时 $P$ 点的坐标;
(3)当 $P C=C O$ 时, 求 $P$ 点坐标.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

在平面直角坐标系 $x O y$ 中, 抛物线 $y=-x^2+b x+c$ 与 $x$ 轴交于
$A(-1,0), B(-3,0)$ 两点, 与 $y$ 轴交于点 $C$.
(1)求抛物线的解析式；
(2)设抛物线的顶点为 $D$, 点 $P$ 在抛物线的对称轴上, 且 $\angle A P D$ $=\angle A C B$, 求点 $P$ 的坐标;
(3)点 $Q$ 是直线 $B C$ 上方抛物线上的动点, 求点 $Q$ 到直线 $B C$的距离最大时点 $Q$ 的坐标.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 抛物线 $y=-x^2+b x+c$ 与 $x$ 轴交于 $A(-1,0), B(5$, 0 )两点, 直线 $y=-\frac{3}{4} x+3$ 与 $y$ 轴交于点 $C$, 与 $x$ 轴交于点 $D$.点 $P$ 是 $x$ 轴上方的抛物线上一动点, 过点 $P$ 作 $P F \perp x$ 轴于点 $F$, 交直线 $C D$ 于点 $E$. 设点 $P$ 的横坐标为 $m$.
(1)求抛物线的解析式;
(2)若 $P E=5 E F$, 求 $m$ 的值；
(3) 若点 $E^{\prime}$ 是点 $E$ 关于直线 $P C$ 的对称点, 是否存在点 $P$, 使点 $E^{\prime}$ 落在 $y$ 轴上? 若存在, 请直接写出相应的点 $P$ 的坐标; 若不存在, 请说明理由.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 过抛物线 $y=\frac{1}{4} x^2-2 x$ 上一点 $A$ 作 $x$ 轴的平行线, 交抛物线于另一点 $B$, 交 $y$ 轴于点 $C$, 已知点 $A$ 的横坐标为 -2 .
(1)求抛物线的对称轴和点 $\mathrm{B}$ 的坐标;
(2)在 $A B$ 上任取一点 $P$, 连接 $O P$, 作点 $C$ 关于直线 $O P$ 的对称点 $D$,
①连接 $B D$, 求 $B D$ 的最小值；
②当点 $D$ 落在抛物线的对称轴上, 且在 $x$ 轴上方时, 求直线 $P D$ 的函数表达式.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 抛物线 $y=x^2+b x+c$ 过点 $A(3,0), B(1,0)$, 交 $y$ 轴于点 $C$, 点 $P$ 是该抛物线上一动点, 点 $P$ 从 $C$ 点沿抛物线向 $A$ 点运动(点 $P$ 不与点 $A$ 重合), 过点 $P$ 作 $P D / / y$ 轴交直线 $A C$于点 $D$.
(1)求抛物线的解析式;
(2)求点 $P$ 在运动的过程中线段 $P D$ 长度的最大值；
(3)在抛物线对称轴上是否存在点 $M$, 使 $|M A-M C|$ 最大? 若存在, 请求出点 $M$ 的坐标; 若不存在, 请说明理由.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图①, 在平面直角坐标系中, 点 $O$ 为坐标原点, 抛物线 $y$ $=a x^2+b x+5$ 与 $x$ 轴交于点 $A$ 、点 $B$, 与 $y$ 轴交于点 $C$. 直线 $y$ $=x+2$ 经过点 $A$, 交抛物线于点 $D, A D$ 交 $y$ 轴于点 $E$, 连接 $C D$, 且 $C D / / x$ 轴.

(1)求抛物线的解析式；
(2)如图②，过点 $A$ 的直线交抛物线第四象限于点 $F$, 若 $\tan \angle$ $B A F=\frac{1}{2}$, 求点 $F$ 的坐标;
(3)在(2)的条件下, $P$ 为直线 $A F$ 上方抛物线上一点, 过点 $P$作 $P H \perp A F$, 垂足为 $H$, 若 $H E=P E$, 求点 $P$ 的坐标.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 抛物线 $y=-x^2+b x+c$ 与 $x$ 轴交于 $A, B$ 两点, 与 $y$轴交于点 $C$, 点 $O$ 为坐标原点, 点 $D$ 为抛物线的顶点, 点 $E$在抛物线上, 点 $F$ 在 $x$ 轴上, 四边形 $O C E F$ 为矩形, 且 $O F=$ $2, E F=3$.
(1)求抛物线的解析式;
(2)连接 $C B$ 交 $E F$ 于点 $M$, 连接 $A M$ 交 $O C$ 于点 $R$, 连接 $A C$,求 $\triangle A C R$ 的周长；
(3)设 $G(4,-5)$ 在该抛物线上, $P$ 是 $y$ 轴上一动点, 过点 $P$ 作 $P H \perp E F$ 于点 $H$, 连接 $A P, G H$, 问 $A P+P H+H G$ 是否有最小值? 如果有, 求出点 $P$ 的坐标; 如果没有, 请说明理由.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, $\triangle M C B$ 的顶点 $B 、 C$ 分别在 $x$ 轴、 $y$ 轴的正半轴上,抛物线 $y=a x^2+b x+c(a \neq 0)$ 经过点 $M, C, B$, 且点 $M$ 为抛物线的顶点, 点 $A(-1,0)$ 是抛物线与 $x$ 轴负半轴的交点, 若线段 $A B=6, \angle A B C=45^{\circ}$.
(1)求抛物线的解析式;
(2)若点 $D$ 为线段 $B M$ 上任意一点(点 $D$ 不与点 $B$ 重合), 过点 $D$ 作垂直于 $x$ 轴的直线 $x=t$, 交抛物线于点 $E$, 交线段 $B C$ 于点 $F$.
①求当 $t$ 为何值时，线段 $D E$ 有最大值? 最大值是多少?
②是否存在这样的点 $D$, 使得 $\frac{E D}{F D}=\frac{1}{2}$ ? 若存在, 求出 $D$ 点的坐标；若不存在, 请说明理由.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 抛物线 $y=\frac{1}{2}(x-3)^2-1$ 与 $x$ 轴交于 $A 、 B$ 两点(点 $A$ 在点 $B$ 的左侧), 与 $y$ 轴交于点 $C$, 顶点为 $D$.
(1)试求点 $A, B, D$ 的坐标；
(2)连接 $C D$, 过原点 $O$ 作 $O E \perp C D$ 与抛物线的对称轴交于点 $E$,求 $O E$ 的长;
(3)以(2)中的点 $E$ 为圆心, 1 为半径画圆, 在对称轴右侧的抛物线上有一动点 $P$, 过点 $P$ 作 $\odot O$ 的切线, 切点为 $Q$, 当 $P Q$的长最小时, 求点 $P$ 的坐标.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 抛物线 $y=a x^2-2 a x+c(a \neq 0)$ 与 $y$ 轴交于点 $C(0,4)$,与 $x$ 轴交于点 $A 、 B$, 点 $A$ 坐标为 $(4,0)$
(1)求抛物线的解析式
(2)抛物线的顶点为 $N$, 在 $x$ 轴上找一点 $K$, 使 $C K+K N$ 最小,并求出点 $K$ 的坐标;
(3)已知 $D$ 是 $O A$ 的中点, 点 $P$ 在第一象限的抛物线上, 过点 $P$ 作 $x$ 轴的平行线, 交直线 $A C$ 于点 $F$, 连接 $O F, D F$. 当 $O F$ $=D F$ 时，求点 $P$ 的坐标.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。