如图①, 在平面直角坐标系中, 点 $O$ 为坐标原点, 抛物线 $y$ $=a x^2+b x+5$ 与 $x$ 轴交于点 $A$ 、点 $B$, 与 $y$ 轴交于点 $C$. 直线 $y$ $=x+2$ 经过点 $A$, 交抛物线于点 $D, A D$ 交 $y$ 轴于点 $E$, 连接 $C D$, 且 $C D / / x$ 轴.

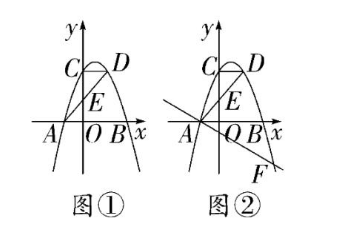
(1)求抛物线的解析式；
(2)如图②，过点 $A$ 的直线交抛物线第四象限于点 $F$, 若 $\tan \angle$ $B A F=\frac{1}{2}$, 求点 $F$ 的坐标;
(3)在(2)的条件下, $P$ 为直线 $A F$ 上方抛物线上一点, 过点 $P$作 $P H \perp A F$, 垂足为 $H$, 若 $H E=P E$, 求点 $P$ 的坐标.