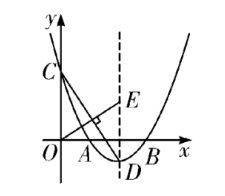
如图, 抛物线 $y=\frac{1}{2}(x-3)^2-1$ 与 $x$ 轴交于 $A 、 B$ 两点(点 $A$ 在点 $B$ 的左侧), 与 $y$ 轴交于点 $C$, 顶点为 $D$.
(1)试求点 $A, B, D$ 的坐标；
(2)连接 $C D$, 过原点 $O$ 作 $O E \perp C D$ 与抛物线的对称轴交于点 $E$,求 $O E$ 的长;
(3)以(2)中的点 $E$ 为圆心, 1 为半径画圆, 在对称轴右侧的抛物线上有一动点 $P$, 过点 $P$ 作 $\odot O$ 的切线, 切点为 $Q$, 当 $P Q$的长最小时, 求点 $P$ 的坐标.