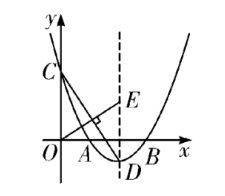
如图, 抛物线
(1)试求点
(2)连接
(3)以(2)中的点
(1)试求点
(2)连接
(3)以(2)中的点
