如图①, 在平面直角坐标系中, 点
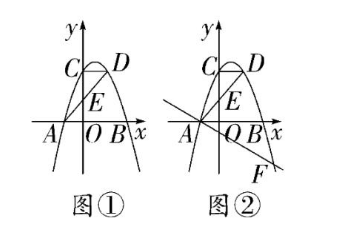
(1)求抛物线的解析式;
(2)如图②,过点
(3)在(2)的条件下,
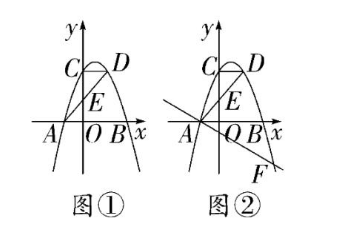
(1)求抛物线的解析式;
(2)如图②,过点
(3)在(2)的条件下,