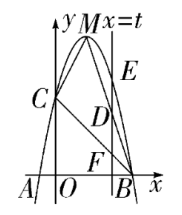如图, $\triangle M C B$ 的顶点 $B 、 C$ 分别在 $x$ 轴、 $y$ 轴的正半轴上,抛物线 $y=a x^2+b x+c(a \neq 0)$ 经过点 $M, C, B$, 且点 $M$ 为抛物线的顶点, 点 $A(-1,0)$ 是抛物线与 $x$ 轴负半轴的交点, 若线段 $A B=6, \angle A B C=45^{\circ}$.
(1)求抛物线的解析式;
(2)若点 $D$ 为线段 $B M$ 上任意一点(点 $D$ 不与点 $B$ 重合), 过点 $D$ 作垂直于 $x$ 轴的直线 $x=t$, 交抛物线于点 $E$, 交线段 $B C$ 于点 $F$.
①求当 $t$ 为何值时，线段 $D E$ 有最大值? 最大值是多少?
②是否存在这样的点 $D$, 使得 $\frac{E D}{F D}=\frac{1}{2}$ ? 若存在, 求出 $D$ 点的坐标；若不存在, 请说明理由.