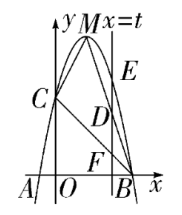如图,
(1)求抛物线的解析式;
(2)若点
①求当
②是否存在这样的点
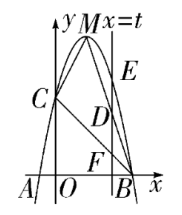
(1)求抛物线的解析式;
(2)若点
①求当
②是否存在这样的点