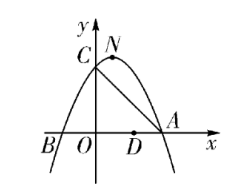
如图, 抛物线 $y=a x^2-2 a x+c(a \neq 0)$ 与 $y$ 轴交于点 $C(0,4)$,与 $x$ 轴交于点 $A 、 B$, 点 $A$ 坐标为 $(4,0)$
(1)求抛物线的解析式
(2)抛物线的顶点为 $N$, 在 $x$ 轴上找一点 $K$, 使 $C K+K N$ 最小,并求出点 $K$ 的坐标;
(3)已知 $D$ 是 $O A$ 的中点, 点 $P$ 在第一象限的抛物线上, 过点 $P$ 作 $x$ 轴的平行线, 交直线 $A C$ 于点 $F$, 连接 $O F, D F$. 当 $O F$ $=D F$ 时，求点 $P$ 的坐标.