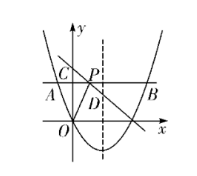
如图, 过抛物线 $y=\frac{1}{4} x^2-2 x$ 上一点 $A$ 作 $x$ 轴的平行线, 交抛物线于另一点 $B$, 交 $y$ 轴于点 $C$, 已知点 $A$ 的横坐标为 -2 .
(1)求抛物线的对称轴和点 $\mathrm{B}$ 的坐标;
(2)在 $A B$ 上任取一点 $P$, 连接 $O P$, 作点 $C$ 关于直线 $O P$ 的对称点 $D$,
①连接 $B D$, 求 $B D$ 的最小值；
②当点 $D$ 落在抛物线的对称轴上, 且在 $x$ 轴上方时, 求直线 $P D$ 的函数表达式.