单选题 （共 12 题 ），每题只有一个选项正确
设集合 $A=\left\{x \mid x^{2}-4 x+3 < 0\right\}, B=\{x \mid 2 x-3>0\}$, 则 $A \cap B= $
$\text{A.}$ $\left(-3,-\frac{3}{2}\right)$
$\text{B.}$ $\left(-3, \frac{3}{2}\right)$
$\text{C.}$ $\left(1, \frac{3}{2}\right)$
$\text{D.}$ $\left(\frac{3}{2}, 3\right)$
设 $(1+i) x=1+y i$, 其中 $x, y$ 是实数, 则 $|x+y i|= $
$\text{A.}$ 1
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ 2
已知等差数列 $\left\{a_{n}\right\}$ 前 9 项的和为 $27, a_{10}=8$, 则 $a_{100}= $
$\text{A.}$ 100
$\text{B.}$ 99
$\text{C.}$ 98
$\text{D.}$ 97
某公司的班车在 7: 00, 8: 00, 8: 30 发车, 小明在 7: 50 至 8: 30 之间到达发车站乘坐班车, 且到达发车站的时刻是随机的, 则他等车时间不 超过 10 分钟的概率是
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{2}{3}$
$\text{D.}$ $\frac{3}{4}$
已知方程 $\frac{x^{2}}{m^{2}+n}-\frac{y^{2}}{3 m^{2}-n}=1$ 表示双曲线, 且该双曲线两焦点间的距 离为 4, 则 $\mathrm{n}$ 的取值范围是（）
$\text{A.}$ $(-1,3)$
$\text{B.}$ $(-1, \sqrt{3})$
$\text{C.}$ $(0,3)$
$\text{D.}$ $(0, \sqrt{3})$
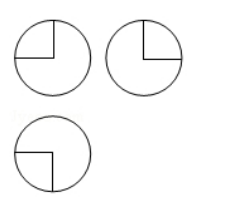
如图, 某几何体的三视图是三个半径相等的圆及每个圆中两条相互 垂直的半径. 若该几何体的体积是 $\frac{28 \pi}{3}$, 则它的表面积是（）
$\text{A.}$ $17 \pi$
$\text{B.}$ $18 \pi$
$\text{C.}$ $20 \pi$
$\text{D.}$ $28 \pi$
函数 $ y=2 x^{2}-e^{|x|} $ 在$[-2,2]$的图象大致为
$\text{A.}$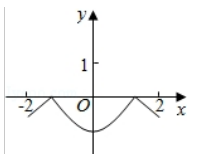 
$\text{B.}$ 
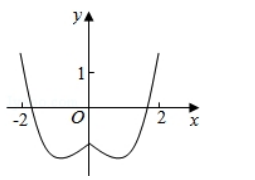$\text{C.}$ 
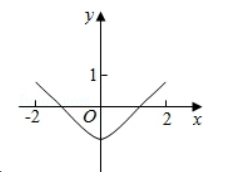$\text{D.}$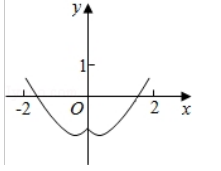 
若 $a>b>1,0 < c < 1$, 则（ )
$\text{A.}$ $\mathrm{a}^{\mathrm{c}} < \mathrm{b}^{\mathrm{c}}$
$\text{B.}$ $a b^{c} < b a^{c}$
$\text{C.}$ $a \log _{\mathrm{b}} \mathrm{c} < \mathrm{blog} \mathrm{a} \mathrm{c}$
$\text{D.}$ $\log _{a} c < \log _{b} c$
执行下面的程序框图, 如果输入的 $x=0, y=1, n=1$, 则输出 $x, y$ 的 值满足（）
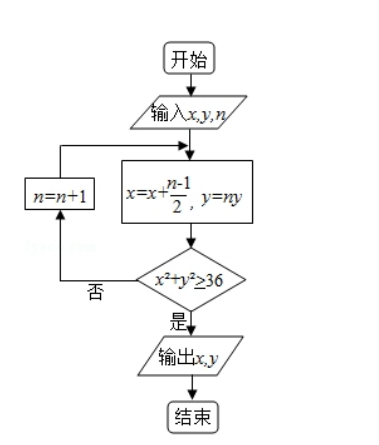
$\text{A.}$ $y=2 x$
$\text{B.}$ $y=3 x$
$\text{C.}$ $y=4 x$
$\text{D.}$ $y=5 x$
以抛物线 $C$ 的顶点为圆心的圆交 $C$ 于 $A 、 B$ 两点, 交 $C$ 的准线于 $D$ 、 $E$ 两点. 已知 $|A B|=4 \sqrt{2},|D E|=2 \sqrt{5}$, 则 $C$ 的焦点到准线的距离为（ )
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ 6
$\text{D.}$ 8
平面 $\alpha$ 过正方体 $\mathrm{ABCD}-\mathrm{A}_{1} \mathrm{~B}_{1} \mathrm{C}_{1} \mathrm{D}_{1}$ 的顶点 $\mathrm{A}, \alpha / /$ 平面 $\mathrm{CB}_{1} \mathrm{D}_{1}, \alpha \cap$面 $A B C D=m, \alpha \cap$ 平面 $A B B_{1} A_{1}=n$, 则 $m 、 n$ 所成角的正弦值为 ( )
$\text{A.}$ $\frac{\sqrt{3}}{2}$
$\text{B.}$ $\frac{\sqrt{2}}{2}$
$\text{C.}$ $\frac{\sqrt{3}}{3}$
$\text{D.}$ $\frac{1}{3}$
已知函数 $f(x)=\sin (\omega x+\phi) \quad\left(\omega>0,|\phi| \leqslant \frac{\pi}{2}\right), x=-\frac{\pi}{4}$ 为 $f($ $x)$ 的零点, $x=\frac{\pi}{4}$ 为 $y=f(x)$ 图象的对称轴, 且 $f(x)$ 在 $\left(\frac{\pi}{18}, \frac{5 \pi}{36}\right)$ 上单调 , 则 $\omega$ 的最大值为（）
$\text{A.}$ 11
$\text{B.}$ 9
$\text{C.}$ 7
$\text{D.}$ 5
填空题 （共 4 题 ），请把答案直接填写在答题纸上
设向量 $\vec{a}=(m, 1), \vec{b}=(1,2)$, 且 $|\vec{a}+\vec{b}|^{2}=|\vec{a}|^{2}+|\vec{b}|^{2}$, 则 $m=$
$(2 x+\sqrt{x})^{5}$ 的展开式中, $x^{3}$ 的系数是 （ ） (用数字填写答案)
设等比数列 $\left\{a_{n}\right\}$ 满足 $a_{1}+a_{3}=10, a_{2}+a_{4}=5$, 则 $a_{1} a_{2} \ldots a_{n}$ 的最大值为
某高科技企业生产产品 $\mathrm{A}$ 和产品 $\mathrm{B}$ 需要甲、乙两种新型材料. 生产 一件产品 $\mathrm{A}$ 需要甲材料 $1.5 \mathrm{~kg}$, 乙材料 $1 \mathrm{~kg}$, 用 5 个工时; 生产一件产品 $\mathrm{B}$ 需 要甲材料 $0.5 \mathrm{~kg}$, 乙材料 $0.3 \mathrm{~kg}$, 用 3 个工时, 生产一件产品 $\mathrm{A}$ 的利润为 2100 元, 生产一件产品 B 的利润为 900 元. 该企业现有甲材料 $150 \mathrm{~kg}$, 乙材料 $90 \mathrm{~kg}$ , 则在不超过 600 个工时的条件下, 生产产品 A、产品 $B$ 的利润之和的最大 值为 （ ） 元.
解答题 （共 8 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
$\triangle \mathrm{ABC}$ 的内角 $\mathrm{A}, \mathrm{B}, \mathrm{C}$ 的对边分别为 $\mathrm{a}, \mathrm{b}, \mathrm{c}$, 已知 $2 \cos C($
$$
a \cos B+b \cos A)=c \text {. }
$$
(1)求 C;
(2) 若 $\mathrm{c}=\sqrt{7}, \triangle \mathrm{ABC}$ 的面积为 $\frac{3 \sqrt{3}}{2}$, 求 $\triangle \mathrm{ABC}$ 的周长.
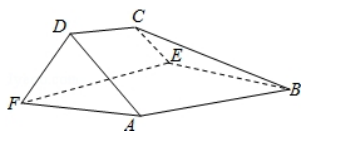
如图, 在以 $A, B, C, D, E, F$ 为顶点的五面体中, 面 $A B E F$ 为正 方形, $A F=2 F D, \angle A F D=90^{\circ}$, 且二面角 $D-A F-E$ 与二面角 $C-B E-F$ 都是 $60^{\circ}$.
(I) 证明平面 $\mathrm{ABEF} \perp$ 平面 $\mathrm{EFDC}$;
(II) 求二面角 $\mathrm{E}-\mathrm{BC}-\mathrm{A}$ 的余弦值.
某公司计划购买 2 台机器, 该种机器使用三年后即被淘汰. 机器 有一易损零件, 在购进机器时, 可以额外购买这种零件作为备件, 每个 200 元. 在机器使用期间, 如果备件不足再购买, 则每个 500 元. 现需决策在购 买机器时应同时购买几个易损零件, 为此搜集并整理了 100 台这种机器在三 年使用期内更换的易损零件数, 得如图柱状图:
以这 100 台机器更换的易损零件数的频率代替 1 台机器更换的易损零件数发生 的概率, 记 $X$ 表示 2 台机器三年内共需更换的易损零件数, $n$ 表示购买 2 台机器的同时购买的易损零件数．
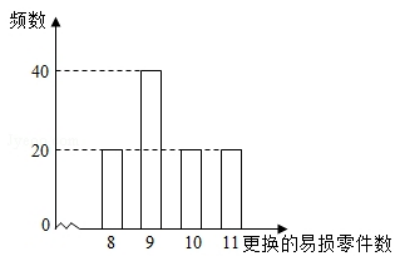
( I ) 求 $\mathrm{X}$ 的分布列;
(II ) 若要求 $P(x \leqslant n) \geqslant 0.5$, 确定 $n$ 的最小值;
(IIII) 以购买易损零件所需费用的期望值为决策依据, 在 $n=19$ 与 $n=20$ 之中选其 一，应选用哪个?
设圆 $x^{2}+y^{2}+2 x-15=0$ 的圆心为 $A$, 直线 | 过点 $B(1,0)$ 且与 $x$ 轴 不重合, I交圆 $A$ 于 $C, D$ 两点, 过 $B$ 作 $A C$ 的平行线交 $A D$ 于点 $E$.
(I) 证明 $|E A|+|E B|$ 为定值, 并写出点 $E$ 的轨迹方程;
(II) 设点 $E$ 的轨迹为曲线 $C_{1}$, 直线 I 交 $C_{1}$ 于 $M, N$ 两点, 过 $B$ 且与 I 垂直的直 线与圆 $A$ 交于 $P, Q$ 两点, 求四边形 MPNQ 面积的取值范围.
已知函数 $f(x)=(x-2) e^{x}+a(x-1) ^2$ 有两个零点.
( I ) 求 $a$ 的取值范围;
(II) 设 $x_{1}, x_{2}$ 是 $f(x)$ 的两个零点, 证明: $x_{1}+x_{2} < 2$.
如图, $\triangle \mathrm{OAB}$ 是等腰三角形, $\angle \mathrm{AOB}=120^{\circ}$. 以 $\mathrm{O}$ 为圆心, $\frac{1}{2} \mathrm{OA}$ 为 半径作圆.
（I）证明：直线 $\mathrm{AB}$ 与 $\odot \mathrm{O}$ 相切;
(II) 点 $C, D$ 在 $\odot O$ 上, 且 $A, B, C, D$ 四点共圆, 证明: $A B / / C D$.
23. 在直角坐标系 $x O y$ 中, 曲线 $C_{1}$ 的参数方程为 $\left\{\begin{array}{l}x=a \operatorname{cost} \\ y=1+\operatorname{asin} t\end{array}\right.$ ( $t$ 为参数, $a>0 ）$
. 在以坐标原点为极点, $x$ 轴正半轴为极轴的极坐标系中, 曲线 $C_{2}: \rho=4 \cos \theta$.
( I ) 说明 $C_{1}$ 是哪种曲线, 并将 $C_{1}$ 的方程化为极坐标方程;
(II) 直线 $C_{3}$ 的极坐标方程为 $\theta=\alpha_{0}$, 其中 $\alpha_{0}$ 满足 $\tan \alpha_{0}=2$, 若曲线 $C_{1}$ 与 $C_{2}$ 的公 共点都在 $C_{3}$ 上, 求 $a$.
已知函数 $f(x)=|x+1|-|2 x-3|$.
( I ) 在图中画出 $\mathrm{y}=\mathrm{f}(\mathrm{x})$ 的图象;
（II ）求不等式 $|f(x)|>1$ 的解集.
