单选题 (共 5 题 ),每题只有一个选项正确
柱状光学器件横截面如图所示, $O P$ 右侧是以 $O$ 为圆心、半径为 $R$ 的 $\frac{1}{4}$ 圆, 左则是直角梯形, $A P$ 长为 $R$, $A C$ 与 $C O$ 夹角 $45^{\circ}, A C$ 中点为 $B \circ a 、 b$ 两种频率的细激光束, 垂直 $A B$ 面入射, 器件介质对 $a, b$ 光的 折射率分别为 $1.42 、 1.40$ 。保持光的入射方向不变, 入射点从 $A$ 向 $B$ 移动过程中, 能在 $P M$ 面全反射后, 从 $O M$ 面射出的光是 (不考虑三次反射以后的光) |

$\text{A.}$ 仅有a光
$\text{B.}$ 仅有b光
$\text{C.}$ a、b光都可以
$\text{D.}$ a、b光都不可以
一点光源以 $113 \mathrm{~W}$ 的功率向周围所有方向均匀地辐射波长约为 $6 \times 10^{-7} \mathrm{~m}$ 的光, 在离点光源距离为R处每秒垂直通过每平方米的光子数为$3 × 10^14$个。普朗克常量为$h = 6.63 × 10^{-34}Js$。R约为
$\text{A.}$ $1 \times 10^2 \mathrm{~m}$
$\text{B.}$ $3 \times 10^2 \mathrm{~m}$
$\text{C.}$ $6 \times 10^2 \mathrm{~m}$
$\text{D.}$ $9 \times 10^2 \mathrm{~m}$
如图所示,王亚平在天宫课堂上演示了水球光学实验,在失重环境下,往大水球中央注入空气,形成了一个空气泡,气泡看起来很明亮,其主要原因是

$\text{A.}$ 气泡表面有折射没有全反射
$\text{B.}$ 光射入气泡衍射形成“亮斑”
$\text{E.}$ 气泡表面有折射和全反射
$\text{F.}$ 光射入气泡干涉形成“亮斑”
关于双缝干涉实验,下列说法正确的是
$\text{A.}$ 用复色光投射就看不到条纹
$\text{B.}$ 明暗相间条纹是两列光在屏上叠加的结果
$\text{C.}$ 把光屏前移或后移,不能看到明暗相间条纹
$\text{D.}$ 蓝光干涉条纹的间距比红光的大
如图所示, 用激光笔照射半圆形玻璃砖圆心 $O$ 点, 发现有 $a 、 b 、 c 、 d$ 四条细光束, 其中 $d$ 是光经折射和 反射形成的。当入射光束 $a$ 绕 $O$ 点逆时针方向转过小角度 $\Delta \theta$ 时, $b 、 c 、 d$ 也会随之转动, 则

$\text{A.}$ 光束 $b$ 顺时针旋转角度小于 $\Delta \theta$
$\text{B.}$ 光束 $c$ 逆时针旋转角度小于 $\Delta \theta$
$\text{C.}$ 光束 $d$ 顺时针旋转角度大于 $\Delta \theta$
$\text{D.}$ 光速 $b 、 c$ 之间的夹角减小了 $2 \Delta \theta$
多选题 (共 2 题 ),每题有多个选项正确
某同学采用图甲所示的实验装置研究光的干涉与衍射现象,狭缝 S1,S2 的宽度可调,狭缝到屏的距离为L。同一单色光垂直照射狭缝,实验中分别在屏上得到了图乙,图丙所示图样。下列描述正确的是
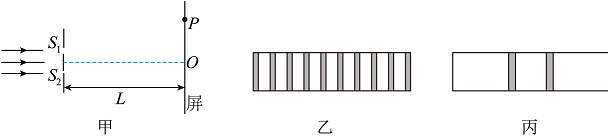
$\text{A.}$ 图乙是光的双缝干涉图样,当光通过狭缝时,也发生了衍射
$\text{B.}$ 遮住一条狭缝,另一狭缝宽度增大,其他条件不变,图丙中亮条纹宽度增大
$\text{C.}$ 照射两条狭缝时,增加L,其他条件不变,图乙中相邻暗条纹的中心间距增大
$\text{D.}$ 照射两条狭缝时,若光从狭缝 S1、S2 到屏上P点的路程差为半波长的奇数倍,P点处一定是暗条纹
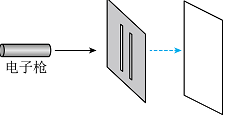
电子双揵干涉实验是近代证实物质波存在的实验。如图所示, 电子枪持续发射的电子动量为
$1.2×10^{-23} kg·m/s$,然后让它们通过双缝打到屏上。已知电子质量取$9.1×10^{-31}$ kg,普朗克常量取$6.6×10^{-34}J·s$,下列说法正确的是
$\text{A.}$ 发射电子的动能约为 $8.0 \times 10^{-15} \mathrm{~J}$
$\text{B.}$ 发射电子的物质波波长约为 $5.5 \times 10^{-11} \mathrm{~m}$
$\text{C.}$ 只有成对电子分别同时通过双缝才能发生干涉
$\text{D.}$ 如果电子是一个一个发射的, 仍能得到干涉图样
解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
一细束单色光在三棱镜 $A B C$ 的侧面 $A C$ 上以大角度由 $D$ 点入射 (入射面在棱镜的横截面内), 入射角为 $i$, 经折射后射至 $A B$ 边的 $E$ 点, 如图所示, 逐渐减小 $i, E$ 点向 $B$ 点移动, 当 $\sin i=\frac{1}{6}$ 时, 恰好没有光线从 $A B$ 边射出棱镜, 且 $D E=D A$ 。求棱镜的折射率。
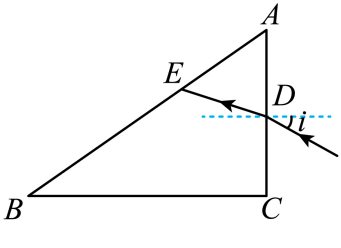
如图, 边长为 $a$ 的正方形 $A B C D$ 为一棱镜的横截面, $M$ 为 $A B$ 边的中点。在截面所在平的, 光线自 $M$ 点 射入棱镜, 入射角为 $60^{\circ}$, 经折射后在 $B C$ 边的 $N$ 点恰好发生全反射, 反射光线从 $C D$ 边的 $P$ 点射出棱镜, 求棱镜的折射率以及 $P 、 C$ 两点之间的距离。
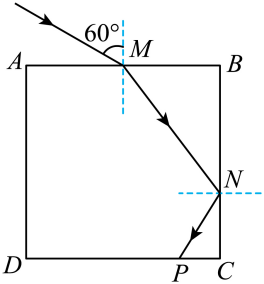
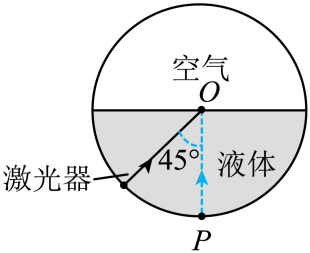
一个水平放置的圆柱形罐体内装了一半的透明液体, 液体上方是空气, 其截面如图所示。一激光器从罐体 底部 P 点沿着罐体的内壁向上移动, 它所发出的光束始终指向圆心 $\mathrm{O}$ 点。当光束与坚直方向成 $45^{\circ}$ 角时, 恰好观察不到从液体表面射向空气的折射光束。已知光在空气中的传播速度为 $c$, 求液体的折射率 $n$ 和激光 在液体中的传播速度 $v$ 。
如图, 某种防窥屏貝透明介质和对光完全吸收的屏障构成, 其中屏障垂直于屏幕平行排列, 可实现对像素
单元可视角度 $\theta$ 的控制 (可视角度 $\theta$ 定义为某像素单元发出的光在图示平面内折射到空气后最大折射角的 2 倍)。透明介质的折射率 $n=2$, 屏障间隙 $L=0.8 \mathrm{~mm}$ 。发光像素单元紧贴屏下, 位于相邻两屏障的正中间. 不 考虑光的衍射。
(1) 若把发光像素单元视为点光源, 要求可视角度 $\theta$ 控制为 $60^{\circ}$, 求屏障的高度 $d$;
(2) 若屏障高度 $d=1.0 \mathrm{~mm}$, 且发光像素单元的宽度不能忽略, 求像素单元宽度 $x$ 最小为多少时, 其可视 角度 $\theta$ 刚好被扩为 $180^{\circ}$ (只要看到像素单元的任意一点, 即视为能看到该像素单元)。

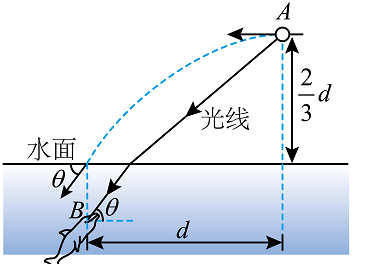
如图所示, 水族馆训练员在训练海豚时, 将一发光小球高举在水面上方的 $A$ 位置, 海豚的眼睛在 $B$ 位置, $A$ 位置和 $B$ 位置的水平距离为 $d, A$ 位置离水面的高度为 $\frac{2}{3} d$ 。训练员将小球向左水平抛出, 入水点在 $B$ 位 置的正上方, 入水前瞬间速度方向与水面夹角为 $\theta_0$ 小球在 $A$ 位置发出的一束光线经水面折射后到达 $B$ 位置, 折射光线与水平方向的夹角也为 $\theta$ 。
已知水的折射率 $n=\frac{4}{3}$, 求:
(1) $\tan \theta$ 的值;
(2) $B$ 位置到水面的距离 $H$ 。
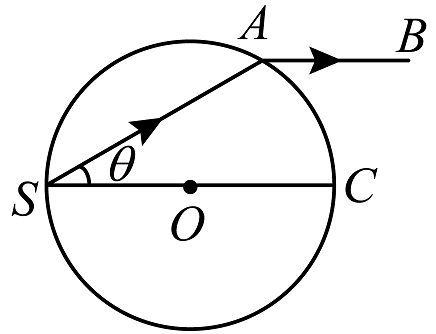
如图, 一个半径为 $R$ 的玻璃球, $O$ 点为球心。球面内侧单色点光源 $S$ 发出的一束光在 $A$ 点射出, 出射光线 $A B$ 与球直径 $S C$ 平行, $\theta=30^{\circ}$ 。光在真空中的传播速度为 $c$ 。求:
(1) 玻璃的折射率;
(2) 从 $S$ 发出的光线经多次全反射回到 $S$ 点的最短时间。
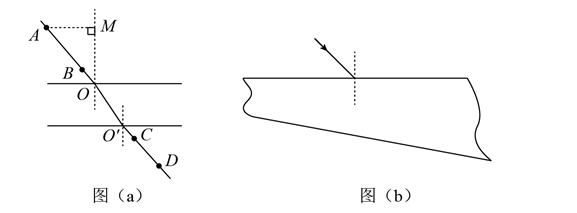
用插针法测量上、下表面平行的玻璃砖的折射率。实验中用 $A 、 B$ 两个大头针确定入射光路、C、D两个大 头针确定出射光路, $O$ 和 $O^{\prime}$ 分别是入射点和出射点, 如图 (a) 所示。测得玻璃砖厚度为 $h=15.0 \mathrm{~mm}, \mathrm{~A}$ 到过 $O$ 点的法线 $O M$ 的距离 $A M=10.0 \mathrm{~mm}, M$ 到玻璃砖的距离 $M O=20.0 \mathrm{~mm}, O^{\prime}$ 到 $O M$ 的距离为 $s=5.0 \mathrm{~mm}$ 。
(i) 求玻璃砖的折射率;
(ii) 用另一块材料相同, 但上下两表面不平行的玻璃砖继续实验, 玻璃砖的截面如图 (b) 所示。光从上 表面入射, 入时角从 0 逐渐增大, 达到 $45^{\circ}$ 时, 玻璃砖下表面的出射光线恰好消失。求此玻璃砖上下表面的 夹角。
我国古代著作 《墨经》中记载了小孔成倒像的实验, 认识到光沿直线传播。身高 $1.6 \mathrm{~m}$ 的人站在水平地面上, 其正前方 $0.6 \mathrm{~m}$ 处的坚直木板墙上有一个圆柱形孔洞, 直径为 $1.0 \mathrm{~cm}$ 、深度为 $1.4 \mathrm{~cm}$, 孔洞距水平地面的高 度是人身高的一半。此时, 由于孔洞深度过大, 使得成像不完整, 如图所示。现在孔洞中填充厚度等于洞 深的某种均匀透明介质,不考虑光在透明介质中的反射。
(i)若该人通过小孔能成完整的像,透明介质的折射率最小为多少?
(ii)若让掠射进入孔洞的光能成功出射, 透明介质的折射率最小为多少?
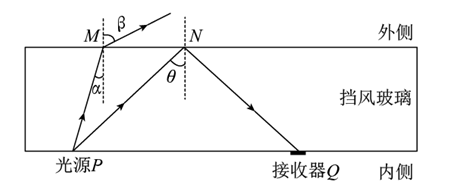
如图所示, 一种光学传感器是通过接收器 $\mathrm{Q}$ 接收到光的强度变化而触发工作的。光从挡风 玻璃内侧 $P$ 点射向外侧 $M$ 点再折射到空气中, 测得入射角为 $\alpha$, 折射角为 $\beta$; 光从 $P$ 点射向外侧 $N$ 点, 刚 好发生全反射并被 $\mathrm{Q}$ 接收, 求光从玻璃射向空气时临界角 $\theta$ 的正弦值表达式。
将两块半径均为 $R$ 、完全相同的透明半圆柱体 $A 、 B$ 正对放置, 圆心上下错开一定距离, 如图所示, 用一束 单色光沿半径照射半圆柱体 $A$, 设圆心处入射角为 $\theta$, 当 $\theta=60^{\circ}$ 时, $A$ 右侧恰好无光线射出; 当 $\theta=30^{\circ}$ 时, 有光线沿 $B$ 的半径射出, 射出位置与 $A$ 的圆心相比下移 $h$, 不考虑多次反射, 求:
(1) 半圆柱体对该单色光的折射率;
(2) 两个半圆柱体之间的距离 $d$ 。
