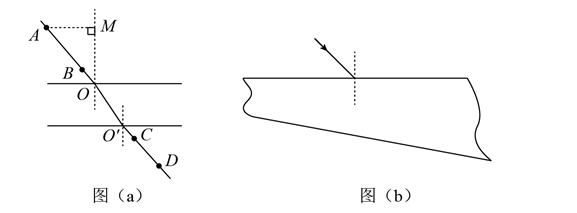
用插针法测量上、下表面平行的玻璃砖的折射率。实验中用 $A 、 B$ 两个大头针确定入射光路、C、D两个大 头针确定出射光路, $O$ 和 $O^{\prime}$ 分别是入射点和出射点, 如图 (a) 所示。测得玻璃砖厚度为 $h=15.0 \mathrm{~mm}, \mathrm{~A}$ 到过 $O$ 点的法线 $O M$ 的距离 $A M=10.0 \mathrm{~mm}, M$ 到玻璃砖的距离 $M O=20.0 \mathrm{~mm}, O^{\prime}$ 到 $O M$ 的距离为 $s=5.0 \mathrm{~mm}$ 。
(i) 求玻璃砖的折射率;
(ii) 用另一块材料相同, 但上下两表面不平行的玻璃砖继续实验, 玻璃砖的截面如图 (b) 所示。光从上 表面入射, 入时角从 0 逐渐增大, 达到 $45^{\circ}$ 时, 玻璃砖下表面的出射光线恰好消失。求此玻璃砖上下表面的 夹角。