单选题 (共 12 题 ),每题只有一个选项正确
$-\sqrt{4}=$
$\text{A.}$ $-2$
$\text{B.}$ $-\frac{1}{2}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $2$
2022 年 5 月, 四川省发展和改革委员会下达了保障性安居工程 2022 年第一批中央预算内投资计划, 泸州市获得 75500000 元中央预算内资金支持, 将 75500000 用科学记数法表示为
$\text{A.}$ $7.55 \times 10^6$
$\text{B.}$ $75.5 \times 10^6$
$\text{C.}$ $7.55 \times 10^7$
$\text{D.}$ $75.5 \times 10^7$
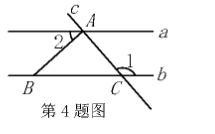
如图, 直线 $a / / b$, 直线 $c$ 分别交 $a, b$ 于点 $A, C$, 点 $B$ 在直线 $b$ 上, $A B \perp A C$, 若 $\angle 1=130^{\circ}$, 则 $\angle 2$ 的度数是
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $40^{\circ}$
$\text{C.}$ $50^{\circ}$
$\text{D.}$ $70^{\circ}$
下列运算正确的是
$\text{A.}$ $a^2 \cdot a^3=a^6$
$\text{B.}$ $3 a-2 a=1$
$\text{C.}$ $\left(-2 a^2\right)^3=-8 a^6$
$\text{D.}$ $a^6 \div a^2=a^3$
费尔兹奖是国际上享有崇高声誉的一个数学奖项, 每四年评选一次, 主要授予年轻的数学家,下面数据是部分获奖者获奖时的年龄(单位:岁) $29,32,33,35,35,40$ , 则这组数据的众数和中位数分别是
$\text{A.}$ 35,35
$\text{B.}$ 34,33
$\text{C.}$ 34,35
$\text{D.}$ 35,34
与 $2+\sqrt{15}$ 最接近的整数是
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ 7
抛物线 $\mathrm{y}=-\frac{1}{2} x^2+x+1$ 经平移后, 不可能得到的抛物线是
$\text{A.}$ $y=-\frac{1}{2} x^2+x$
$\text{B.}$ $y=-\frac{1}{2} x^2-4$
$\text{C.}$ $y=-\frac{1}{2} x^2+2021 x-2022$
$\text{D.}$ $y=-x^2+x+1$
已知关于 $x$ 的方程 $x^2-(2 \mathrm{~m}-1) x+\mathrm{m}^2=0$ 的两实数根为 $x_1, x_2$, 若 $\left(x_1+1\right)\left(x_2+1\right)=3$, 则 $\mathrm{m}$ 的值为
$\text{A.}$ $-3$
$\text{B.}$ $-1$
$\text{C.}$ $-3$ 或$1$
$\text{D.}$ $-1$ 或$3$
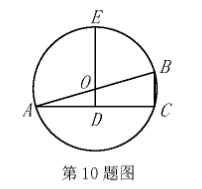
如图, $\mathrm{AB}$ 是 $\odot 0$ 的直径, $O D$ 垂直于弦 $\mathrm{AC}$ 于点 $\mathrm{D}, \mathrm{D} O$ 的延长线交 $\odot O$ 于点 $\mathrm{E}$. 若 $\mathrm{AC}=4 \sqrt{2}, \mathrm{DE}=4$, 则 $\mathrm{BC}$ 的长是
$\text{A.}$ 1
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ 2
$\text{D.}$ 4
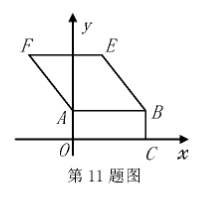
如图, 在平面直角坐标系 $x O \mathrm{y}$ 中, 矩形 $O A B C$ 的顶点 $\mathrm{B}$ 的坐标为 $(10,4)$, 四边形 $\mathrm{ABEF}$ 是菱形, 且 $\tan \angle \mathrm{ABE}=\frac{4}{3}$. 若直线 $l$ 把矩形 $O \mathrm{ABC}$ 和菱形 $\mathrm{ABEF}$ 组成的图形的面积 分成相等的两部分, 则直线 $l$ 的解析式为
$\text{A.}$ $y=3 x$
$\text{B.}$ $y=-\frac{3}{4} x+\frac{15}{2}$
$\text{C.}$ $y=-2 x+11$
$\text{D.}$ $y=-2 x+12$
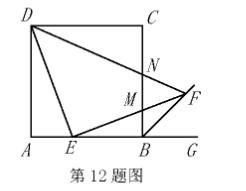
如图, 在边长为 3 的正方形 $A B C D$ 中, 点 $E$ 是边 $A B$ 上的点, 且 $B E=2 A E$, 过点 $E$ 作 $\mathrm{DE}$ 的垂线交正方形外角 $\angle \mathrm{CBG}$ 的平分线于点 $\mathrm{F}$, 交边 $\mathrm{BC}$ 于点 $\mathrm{M}$, 连接 $\mathrm{DF}$ 交边 $\mathrm{BC}$ 于 点 $N$, 则 $M N$ 的长为
$\text{A.}$ $\frac{2}{3}$
$\text{B.}$ $\frac{5}{6}$
$\text{C.}$ $\frac{6}{7}$
$\text{D.}$ $1$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
若 $(a-2)^2+|b+3|=0$, 则 $a b=$
若方程 $\frac{x-3}{x-2}+1=\frac{3}{2-x}$ 的解使关于 $x$ 的不等式 (2-a) $x-3>0$ 成立, 则实数 a 的取值范围 是
如图, 在 Rt $\triangle \mathrm{ABC}$ 中, $\angle C=90^{\circ}, A C=6, B C=2 \sqrt{3}$, 半径为 1 的 $\odot O$ 在 Rt $\triangle \mathrm{ABC}$ 内平移 ( $\odot O$ 可以与该三角形的边相切), 则点 $\mathrm{A}$ 到 $\odot O$ 上的点的距离的最大值为

解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $(\sqrt{3})^0+2^{-1}+2 \cos 45^{\circ}-\left|-\frac{1}{2}\right|$.
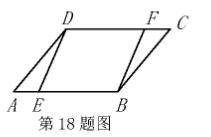
如图, $E, F$ 分别是 $\square A B C D$ 的边 $A B, C D$ 上的点, 已知 $\mathrm{AE}=\mathrm{CF}$.
求证: $\mathrm{DE}=\mathrm{BF}$.
化简: $\left(\frac{m^2-3 m+1}{m}+1\right) \div \frac{m^2-1}{m}$.
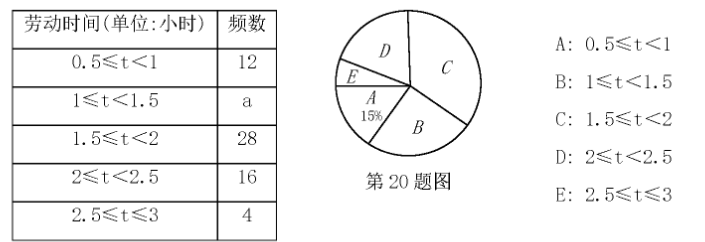
劳动教育具有树德、增智、强体、育美的综合育人价值, 有利于学生树立正确的劳 动价值观. 某学校为了解学生参加家务劳动的情况, 随机抽取了 $\mathrm{m}$ 名学生在某个休 息日做家务的劳动时间作为样本, 并绘制了以下不完整的频数分布表和扇形统计图. 根据题中已有信息, 解答下列问题:
某经销商计划购进 $\mathrm{A}, \mathrm{B}$ 两种农产品. 已知购进 $\mathrm{A}$ 种农产品 2 件, B 种农产品 3 件, 共需 690 元; 购进 $A$ 种农产品 1 件, B种农产品 4 件, 共需 720 元.
(1)A,B两种农产品每件的价格分别是多少元?
(2) 该经销商计划用不超过 5400 元购进 A, B 两种农产品共 40 件, 且. A 种农产品的 件数不超过 B 种农产品件数的 3 倍. 如果该经销商将购进的农产品按照 A 种每件 160 元, B 种每件 200 元的价格全部售出, 那么购进 A, B 两种农产品各多少件时获 利最多?
如图, 直线 $\mathrm{y}=-\frac{3}{2} x+\mathrm{b}$ 与反比例函数 $\mathrm{y}=\frac{12}{x}$ 的图象相交于点 $\mathrm{A}, \mathrm{B}$, 已知点 $\mathrm{A}$ 的纵坐标 为 6 .
(1)求 b 的值;
(2) 若点 $\mathrm{C}$ 是 $x$ 轴上一点, 且 $\triangle \mathrm{ABC}$ 的面积为 3 , 求点 $\mathrm{C}$ 的坐标.

如图, 海中有两小岛 $\mathrm{C}, \mathrm{D}$, 某渔船在海中的 $\mathrm{A}$ 处测得小岛 $\mathrm{C}$ 位于东北方向, 小岛 D 位于南偏东 $30^{\circ}$ 方向, 且 A, D 相距 $10 \mathrm{nmile}$. 该渔船自西向东航行一段时间后到 达点 $\mathrm{B}$, 此时测得小岛 $\mathrm{C}$ 位于西北方向且与点 $\mathrm{B}$ 相距 $8 \sqrt{2} \mathrm{n}$ mile. 求 $\mathrm{B}, \mathrm{D}$ 间的距离 (计算过程中的数据不取近似值).

如图, 点 $C$ 在以 $A B$ 为直径的 $\odot 0$ 上, $C D$ 平分 $\angle A C B$ 交 $\odot 0$ 于点 $D$, 交 $A B$ 于点 $E$, 过 点 $D$ 作 $\odot 0$ 的切线交 $C 0$ 的延长线于点 $F$.
(1)求证: $F D / / A B$;
(2) 若 $A C=2 \sqrt{5}, B C=\sqrt{5}$, 求 $F D$ 的长.

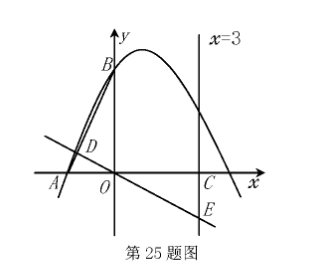
如图, 在平面直角坐标系 $x 0 \mathrm{y}$ 中, 已知抛物线 $\mathrm{y}=\mathrm{a} x^2+x+\mathrm{C}$ 经过 $\mathrm{A}(-2,0), \mathrm{B}(0,4)$ 两点, 直线 $x=3$ 与 $x$ 轴交于点 $\mathrm{C}$.
(1) 求 $\mathrm{a}, \mathrm{c}$ 的值;
(2) 经过点 0 的直线分别与线段 $A B$, 直线 $x=3$ 交于点 $D, E$, 且 $\triangle B D O$ 与 $\triangle O C E$ 的面 积相等, 求直线 DE 的解析式;
(3) $\mathrm{P}$ 是抛物线上位于第一象限的一个动点, 在线段 $\mathrm{OC}$ 和直线 $x=3$ 上是否分别存在 点 $F, G$, 使 $B, F, G, P$ 为顶点的四边形是以 $B F$ 为一边的矩形? 若存在, 求出点 $F$ 的坐标; 若不存在, 请说明理由.